5. Cvičení 5: Potlačení harmonického rušení pomocí ALE

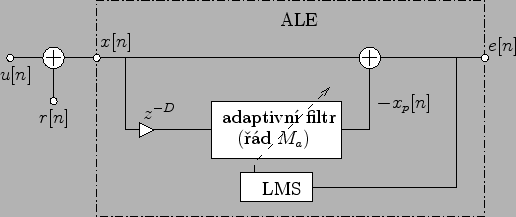
Struktura ALE (Adaptive Line Enhancer) je Obr. 5.1

Figure 5.1: Struktura ALE

Jedná se vlastně o LMS prediktor. Oproti Obr. 3.2 je uvedená struktura trochu obecnější. Předně umožňuje volit zpoždění $D$ ve větvi s adaptivním filtrem (u Obr. 3.2 je toto zpoždění omezeno pouze na jeden vzorek). Dále struktura Obr. 3.2 byla uvedena pro fixní řád adaptivního filtru. Tento rozdíl však není tak podstatný, neboť odvození rovnic bylo provedeno pro obecný řád.

Jelikož jsem v minulých cvičeních používal označení $M$ pro řád celé struktury prediktoru, učiním tak i nyní. Řád adaptivního filtru označím $M_{a}$. Platí tedy

$$M = D + M_{a}.$$

V tomto cvičení se pomocí ALE budeme snažit potlačit harmonické rušení (rušení nemusí být zrovna harmonické, důležité je aby i vzdálenější vzorky rušení byly silně korelovány).

Nicméně úloha se dá různě modifikovat. Můžeme otočit úlohu užitečného signálu a rušení. Například budeme chtít získat harmonický signál (může se jednat o nějakou modulaci). V tomto případě je pro nás výstupem predikce $x_p[n]$. Nebo můžeme chtít určit frekvenci harmonického signálu (to jsme zkoušeli na 3. cvičení).

Označíme vektory

$$\begin{gathered}\mathbf{x}^T[n-D] = [ x[n-D], \ldots ,x[n-M] ... ...\mathbf{w}^T[n] = [ w_1[n], \ldots ,w_{M+1}[n] ] \end{gathered}$$ (5.1)

Odvození rovnic filtrace a úpravy vah kopíruje odvození u Obr. 3.2. Uvedu zde tedy pouze rovnici filtrace viz. Obr. 5.1

$$e[n] = x[n] + \mathbf{w}^T[n] \mathbf{x}[n-D],$$ (5.2)

a úpravy vah

$$\mathbf{w}[n+1] = \mathbf{w}[n] - \mu e[n]\mathbf{x}[n-D].$$ (5.3)

Cvičení 5.0:

5.0.0.0.1 Modelování vstupního signálu:

Užitečný signál volte nulový. Vygenerujte si harmonické rušení s efektivní hodnotou 1 a frekvencí $\frac{\pi}{4}$. Délku obou posloupností volte $N=500$ vzorků. S pomocí $u[n]$ a $r[n]$ vygenerujte vstupní signál $x[n]$, viz. Obr. 5.1.

5.0.0.0.2 ALE:

Napište skript v Matlabu implementující strukturu ALE viz. Obr. 5.1. Volte zpoždění $D = 1$ a řád filtru

A

$M_{a} = 1$ ($M = 2$)

B

$M_{a} = 9$ ($M=10$)

Pro obě volby řádu: Vyneste modul spektra výstupního signálu $x[n]$ a výstupu $e[n]$. Vyneste si frekvenční charakteristiku prediktoru (ALE) pro ustálené váhy (rovněž nuly a póly v z-rovině). Dále průběhy vah adaptivního filtru. Jakým způsobem se zvýšení řádu projevilo?

Uvádím zde skript pro generování vstupního signálu:

N = 500;

% uzitecny signal
u = zeros(N,1); % nulovy

% ruseni
n = 1:N;
Wr = pi/4;
r = sqrt(2)*sin(Wr*n'); % efektivni hodnota 1

% vstupni signal
x = u + r;

Skript implementující ALE napište sami, viz. Obr. 5.1 a rovnice (5.2), (5.3). Nevíte-li si rady vzpomeňte si (podívejte se) na 3. cvičení, kde jsem uváděl skript pro prediktor (odlišnost je pouze v možnosti nastavit jiná zpoždění pomocí $D$). Zde uvedu pouze skript pro vynesení výsledků:

figure(1)
subplot(4,2,1); % vyneseni modulovych spekter pri
                % zachovani meritek os
W = linspace(0,2*pi,N);
plot(W/pi,abs(fft(x)),'b-');
xlabel('W/pi')
ylabel('|X|')
osy = axis;
subplot(4,2,3);
plot(W/pi,abs(fft(e)),'r-');
xlabel('W/pi')
ylabel('|E|')
axis(osy);

subplot(2,2,3); % vyneseni modulovych frekvencnich charakteristik
                % (v ustalenem stavu) |H(exp(j*W))| (celeho ALE)
                % a |H_a(exp(j*W))| (adaptivniho filtru)
WN =100;
W = linspace(0,2*pi,WN);
B = [1; zeros(D-1,1); w(:,N)];
A = [1; zeros(M,1) ];
H = freqz(B,A,W);
plot(W/pi,abs(H),'b-');
hold on
B_a = [ w(:,N) ];
A_a = [ 1; zeros(M_a,1) ];
H_a = freqz(B_a,A_a,W);
plot(W/pi,abs(H_a),'r-');
plot(W/pi,ones(WN,1),'g-');
hold off
xlabel('W/pi')
ylabel('|H| (modre), |H_a| (cervene)')

Výsledky:

Figure 5.2: Řád adaptivního filtru $M_a = 1$ ($M = 2$): (zleva doprava) moduly spekter vstupu $x[n]$ a výstupu $e[n]$, průběh vah, moduly frekvenčních charakteristik celého ALE $H(e^{\jmath \Theta })$ a adaptivního filtru $H_a(e^{\jmath \Theta })$ v ustáleném stavu, rozmístění nul a pólů přenosové funkce $H(z)$ (celé ALE) v z-rovině v ustáleném stavu

Figure 5.3: Řád adaptivního filtru $M_a = 9$ ($M=10$): (zleva doprava) moduly spekter vstupu $x[n]$ a výstupu $e[n]$, průběh vah, moduly frekvenčních charakteristik celého ALE $H(e^{\jmath \Theta })$ a adaptivního filtru $H_a(e^{\jmath \Theta })$ v ustáleném stavu, rozmístění nul a pólů přenosové funkce $H(z)$ (celé ALE) v z-rovině v ustáleném stavu

Cvičení 5.1: Zpoždění $D$ a řád $M_{a}$ volte jako v předchozím cvičení. Užitečný signál $u[n]$ nyní modelujte jako bílý gausovský proces s nulovou střední hodnotou. Varianci užitečného signálu volte podle řádu adaptivního filtru: $\sigma _u^2 = 0.3^2$ pro řád $M_{a} = 1$ a $\sigma_u^2 = 1$ pro řád $M_{a} = 9$ (uvidíte, že u vyššího řádu si můžete dovolit vyšší rozptyly $\sigma_u^2$).

Vyneste výsledky a porovnejte jako v cvičení 1 (všimněte si rozmístění nul a pokuste se ho vysvětlit). Vypočtěte porovnejte (pro obě volby $M_{a}$) dosažené SNRE (Signal to Noise Ratio Enhancement). Dále si vyneste predikci $x_p[n]$ (výstup při obrácení úlohy užitečného a rušivého signálu).

Pro výpočet SNRE uvádím skript. Je hodně zjednodušený například se zde započítává i přechodový děj na začátku, dále případné zesílení nebo zkreslení vstupního signálu se započítává do výkonu šumu (na druhou stranu i tyto věci nám mohou vadit a přesnější výpočet SNRE by nám je utajil)

Pu1 = sum(u.^2)/N;     % výkon uzitecneho sig. na vstupu
Pn1 = sum((x-u).^2)/N; % výkon ruseni na vstupu
Pu2 = sum(u.^2)/N;     % výkon uzitecneho sig. na vystupu
Pn2 = sum((e-u).^2)/N; % výkon ruseni na vystupu
SNR1 = 10*log(Pu1/Pn1);
SNR2 = 10*log(Pu2/Pn2);
SNRE = SNR2-SNR1;

% kdyz nechcete vysledky lovit v promptu Matlabu
% muzete si je vepsat do titulku nejakeho obrazku napriklad tito zpusobem:
title(['SNR1 = ' num2str(SNR1) ', SNR2 = ' num2str(SNR2) ', SNRE = ' num2str(SNRE)]);

Výsledky:

Figure 5.4: Řád adaptivního filtru $M_a = 1$ ($M = 2$), rozptyl užitečného signálu (bílý šum) je $\sigma _u^2 = 0.3^2$ : (zleva doprava) moduly spekter vstupu $x[n]$ a výstupu $e[n]$ (v titulku jsou uvedena SNR a SNRE), průběh vah, moduly frekvenčních charakteristik celého ALE $H(e^{\jmath \Theta })$ a adaptivního filtru $H_a(e^{\jmath \Theta })$ v ustáleném stavu, rozmístění nul a pólů přenosové funkce $H(z)$ (celé ALE) v z-rovině v ustáleném stavu

Figure 5.5: Řád adaptivního filtru $M_a = 9$ ($M=10$), rozptyl užitečného signálu (bílý šum) je $\sigma _u^2 = 1.0$ : (zleva doprava) moduly spekter vstupu $x[n]$ a výstupu $e[n]$ (v titulku jsou uvedena SNR a SNRE), průběh vah, moduly frekvenčních charakteristik celého ALE $H(e^{\jmath \Theta })$ a adaptivního filtru $H_a(e^{\jmath \Theta })$ v ustáleném stavu, rozmístění nul a pólů přenosové funkce $H(z)$ (celé ALE) v z-rovině v ustáleném stavu

Figure 5.6: Řád adaptivního filtru $M_a = 9$ ($M=10$), rozptyl užitečného signálu (bílý šum) je $\sigma _u^2 = 1.0$ : porovnání vstupního signálu $x[n]$ a predikce $x_p[n]$ (všimněte si že, predikce se více podobá harmonickému signálu)

Poznámka: Tím, že adaptivní filtr propustí harmonické rušení (tak aby se na chybovém výstupu $e[n]$ vykompenzovalo) umožní minimalizaci rozptylu na chybovém výstupu ( $\mathrm{E}[e^2[n]]$). Kompenzace je zde možná, protože harmonické rušení se dá velice dobře predikovat ^5.1, neboť jeho vzorky jsou silně korelovány (víme, že na bezchybnou predikci čistého harmonického signálu stačí prediktor 2. řádu).

Tento způsob však nefunguje pro bílý šum $u[n]$, neboť jeho korelace mezi různými vzorky je vždy nulová. Bílý šum se proto nedá vůbec predikovat (nejlepší predikce je 0 - jakákoli netriviální lineární kombinace minulých vzorků dává horší (větší) $\mathrm{E}[e^2[n]]$). Adaptivní filtr se tedy snaží $u[n]$ co nejvíce potlačit (docílit nulové predikce).

Pravdivost těchto výroků se dá velice dobře ilustrovat na vynesených frekvenčních charakteristikách. Vidíme, že adaptivní filtr v ustálení pro vyšší řád propouští takřka pouze harmonické rušení (se zesílením 1), viz. frekvenční charakteristika adaptivního filtru na Obr. 5.5 a predikce Obr. 5.6.

Cvičení 5.2: Stáhněte si řečový signál a použijte ho jako užitečný signál $u[n]$. Řád adaptivního filtru volte $M_{a} = 9$.

Zpoždění $D$ volte

1

$D = 1$ ($M=10$)

2

$D = 11$ ($M = 20$)

Poslechněte si užitečný signál $u[n]$, vstupní signál $x[n]$ (směs), výstup $e[n]$ a vyneste si spektrogramy. Rovněž určete dosažená SNRE.

Vyneste si autokorelační funkci pro řečový signál $u[n]$. Jaká volba $D$ je optimální? Ověřte optimální volbu $D$ výpočtem SNRE.

Uvádím zde skript pro vynesení spektrogramů pro $u[n]$,$x[n]$ a $e[n]$, který zachovává přiřazení barev.

[U,F,T] = specgram(u);
Ul = 20*log(abs(U));
[X,F,T] = specgram(x);
Xl = 20*log(abs(X));
[E,F,T] = specgram(e);
El = 20*log(abs(E));
T = 2*T; % napraveni casove osy u specgram
maxl = max(max([Ul;Xl;El])); % trochu náročné, ale krátké
minl = min(min([Ul;Xl;El]));
Ul = (Ul-minl)/(maxl-minl);
Xl = (Xl-minl)/(maxl-minl);
El = (El-minl)/(maxl-minl);

subplot(2,2,1);
imagesc(T,F,Ul);
caxis([0,1]);
axis('xy');
xlabel('n');
ylabel('|U| [dB]');
subplot(2,2,2);
imagesc(T,F,Xl);
caxis([0,1]);
axis('xy');
xlabel('n');
ylabel('|X| [dB]');
subplot(2,2,3);
imagesc(T,F,El);
caxis([0,1]);
axis('xy');
xlabel('n');
ylabel('|E| [dB]');

Figure 5.7: Řád adaptivního filtru $M_a = 9$, zpoždění $D = 1$ ($M=10$): (zleva doprava) Spektrogram $u[n]$ - čistá řeč (v titulku jsou uvedena SNR a SNRE), Spektrogram $x[n]$ (směs na vstupu), Spektrogram $e[n]$ (výstup), průběh vah

Figure 5.8: Řád adaptivního filtru $M_a = 9$, zpoždění $D = 11$ ($M = 20$): (zleva doprava) Spektrogram $u[n]$ - čistá řeč (v titulku jsou uvedena SNR a SNRE), Spektrogram $x[n]$ (směs na vstupu), Spektrogram $e[n]$ (výstup), průběh vah

Poznámka: Všimněte si, že pro $D = 1$ je řečový signál na výstupu $e[n]$ výrazně potlačen (oproti vstupu $x[n]$), viz. moduly spekter, dosažené SNRE a spektrogramy na Obr. 5.7. Je to tím, že blízké vzorky řeči jsou významně korelovány (narozdíl od bílého šumu v předchozím cvičení). Vzpomeňte si, jak jste na 2. cvičení modelovali řeč jako AR proces 10. řádu.

Pro $D = 11$ můžete pozorovat výrazné zlepšení, viz. moduly spekter, dosažené SNRE a spektrogramy na Obr. 5.8. Důvod je ten, že korelace mezi příspěvkem řeči na vstupu $u[n]$ a na zpožděních adaptivního filtru $u[n-D],\ldots,u[n-M]$ již není tak vysoká. Řeč se tedy pro $D = 11$ hůře predikuje než pro $D = 1$ a proto se na chybovém výstupu hůře kompenzuje.

Čím méně jsou příspěvky užitečného signálu $u[n]$ korelovány s příspěvky užitečného signálu na zpožděních adaptivního filtru tím lepších výsledků dosáhneme. Tento fakt je ilustrován na porovnání průběhů autokorelační funkce řečového signálu $u[n]$: $r_{uu,k}$, $k=1,2,\ldots$ a závislosti dosaženého SNRE na zpoždění $D$ uvedeném na Obr. 5.9.

Figure 5.9: Řád adaptivního filtru $M_a = 9$: Porovnání průběhů autokorelační funkce řečového (užitečného) signálu $u[n]$ a závislosti dosaženého SNRE na zpoždění $D$.