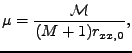7.1 LMS

První cvičení věnujeme vlivu volby $\mu$ (4.1) na chování LMS algoritmu. Konvergenční konstantu $\mu$ volíme podle vztahu

$$\mu = \frac{\mathcal{M}}{(M+1) r_{xx,0}} ,$$ (7.1)

kde $(M+1)$ má význam počtu vah adaptivního filtru ($M$ je řád adaptivního filtru), $r_{xx,0}$ označuje výkon (rozptyl vstupního signálu $x[n]$ - předpokládáme nulovou střední hodnotu $x[n]$). Parametr $\mathcal{M}$ (Missadjustment) udává o kolik se zvýší výkon (rozptyl) chybového signálu $\mathrm{E}[e^2[n]]$ (MSE) v důsledku gradientního šumu vah v ustáleném stavu. Například hodnota $\mathcal{M}=0.1$ má význam zvýšení MSE o $10\%$ atd.. Rozumné volby $\mathcal{M}$ jsou zhruba do $30\%$, pro vyšší $\mathcal{M}$ přestává (7.1) platit. Efekt volby $\mathcal{M}$ ($\mu$) jste si již mnohokrát ověřili. Čím větší $\mathcal{M}$ zvolíme, tím rychleji LMS konverguje do ustáleného stavu. Bohužel také tím větší rozptyl vykazuje průběh vah v ustáleném stavu (gradientní šum), což se projevuje zvýšením MSE.

Cvičení 7.0: Přenosovou funkci identifikovaného systému volte plant_A = [1;0]; plant_B = [-1;-3] . Aditivní rušení $u[n]$ budeme opět modelovat bílým stacionárním gausovským procesem s nulovou střední hodnotou. Rozptyl $u[n]$ volte $\sigma_u^2 = 5$. Vstupní signál $x[n]$ modelujte jako bílý stacionární gausovský proces s nulovou střední hodnotou a rozptylem 1.

Porovnejte průběhy MSE $\mathrm{E}[e^2[n]]$ LMS algoritmu pro volbu Missadjustmentu $\mathcal{M}=0.03$ a $\mathcal{M}=0.2$.

Pro výpočet MSE atd., je potřeba více realizací. Skripty pro tyto účely jste si již vytvořili ve cvičení 4 (viz. cvičení 4.2). Zde se hodí skripty pro generování více realiací trochu upravit, neboť vždy budeme porovnávat dva typy algoritmů (nebo dvě verze téhož s různým nastavením) proti sobě., rovněž budu pořebovat uchovávat hodnoty vah. Je tedy vhodné vše držet ve dvou sadách (realizace budících signálů, realizace vah, adt.). Uvedu zde příklad skriptu pro generování realizací chybového signálu:

E1 = zeros(N,R); W1 = zeros(M+1,N,R);
E2 = zeros(N,R); W2 = zeros(M+1,N,R);

for r=1:R

  x = X1(:,r); d = D1(:,r);
  MissAdj = 0.03;
  lms;
  E1(:,r) = e; W1(:,:,r) = w;

  x = X2(:,r); d = D2(:,r);
  MissAdj = 0.2; % volba mu
  lms;
  E2(:,r) = e; W2(:,:,r) = w;

end; % r

skript pro generování dvou sad realizací $x[n]$ a $d[n]$ zde neuvádím (jejich realizace je vhodné držet rovněž ve dvou sadách neboť budem porovnávat vliv buzení bílým a barevným šumem). Počet realizací vlote $R=500$ (na odlaďování satčí $R=50$). Opakuji, že střední hodnotu ve výpočtu MSE ( $\mathrm{E}[e^2[n]]$) je nutno aplikovat tak jak je psáno, čili pouze přes realizace nikoli přes čas ($e[n]$ není stacionární). Skript pro výpočet MSE byl uveden ve cvičení 4.2.

Výsledky:

Figure: LMS: Porovnání průběhů MSE pro různé volby Missadjustmentu $\mathcal{M}=0.03$ a $\mathcal{M}=0.2$

Je zřejmé (viz. Obr. 4.2), že v ustáleném stavu by mělo na chybový výstup $e[n]$ projít pouze adidivní rušení $u[n]$, vstupní signál $x[n]$ by se měl na chybovém výstupu vykompenzovat (při přesném nastavení vah). Tedy ideálně (žádný gradientní šum) by mělo být MSE na výstupu rovno rozptylu aditivního rušení $\sigma_u^2$ (proto vynáším MSE normovaně $\mathrm{MSE}/\sigma_u^2$). Ověřte si, že vztah (7.1) opravdu funguje. $\mathcal{M}=0.2$ by mělo odpovídat $\mathrm{MSE}/\sigma_u^2 = 1.2$ atd..

Cvičení 7.1: Porovnejte průběh MSE na čase a trajektorii vah ve váhovém prostoru (vyneste si rovněž vrstevnice chybového povrchu) pro LMS při buzení bílým gausovským šumem (stejné buzení jako v předešlém cvičení 7.1) a barevným šumem (AR 2. řádu s normovaným rozptylem na 1 stejně jako ve cvičení 4 pouze moduly obou pólů nastavte na $0.7$). Konvergenční konstantu $\mu$ volte v obou případech stejně a to tak aby $\mathcal{M}=0.1$. Rozptyl aditivního šumu volte v obou případech $\sigma _u^2 = 0.3^2$.

MSE je vhodné vynášet logaritmicky, pak byste měli u barevného buzení jasně rozlišit dva sklony (dvě časové konstanty). Proč LMS pro barevné buzení konverguje s dvěma časovými konstantami je vidět z chybových povrchů. Co je to chybový povrch a jak se spočítá je uvedeno podrobně v 4.3. Pokud jste se k tomu ještě nedostali doporučuji nyní přečíst.

Jak víte, chybový povrch $\mathrm{E}[e^2[n]](\mathbf{w})$ je funkcí váhového vektoru. Můžeme ho napočítat pouze pro konečně monoho hodnot $\mathbf{w}$. Omezíme se tedy na body v nějakém intervalu. Ten zvolíme tak, aby pokud možno obsahoval počáteční nastavení $[0;0]$ a hodnoty vah v ustálení $[-1;-3]$. Například $(-3,2)\times(-4,1)$. Zde uvádím skript (indexování sady jsem pro přehlednost vynechal)

esN = 100;
w1R = linspace(-3,2,esN);
w2R = linspace(-4,1,esN);
es = zeros(esN,esN);
for i1 = 1:esN
for i2 = 1:esN
  w = [w1R(i1);w2R(i2)];
  es1(i2,i1) = ... % doplnte
end
end

Pro výpočet es(i1,i2) ( $\mathrm{E}[e^2[n]](\mathbf{w})$) můžete použít rovnici (4.4). Musíte ale nejprve odhadnout $\mathbf{R}_{xx}$, $\mathbf{r}_{xd}, r_{dd,0}$ viz. komentář u (4.4). Do obrázku si pak vyneste vrstevnice chybového povrchu, několik realizací trajektorií váhového vektotu a rovněž $\mathrm{E}[\mathbf{w}[n]]$.

figure(1)                     % pouze pro 1. sadu
contour(w1R,w2R,10*log(es1)); % vrstevnice (nerovnomerne - log)
hold on
for r = 1:5                   % 5 realizaci
plot(W1(1,M+1:N-1,r),W1(2,M+1:N-1,r),'b-');
end;
Wmean1 = sum(W1,3)/R;         % stredni hodnota
plot(Wmean1(1,M+1:N-1),Wmean1(2,M+1:N-1),'r-');
hold off
axis square                   % rotacni paraboloid by mel vypadat jako rotacni
xlabel('w1');
ylabel('w2');
title('popisek');

Výsledky:

Figure: LMS ( $\mathcal{M}=0.1$): Porovnání průběhů MSE a chybových povrchů pro buzení bílým šumem a barevné buzení

Vysvětlení rozdílné konvergence LMS při buzení bílým a barevným šumem je uvedeno v 4.3. Již poněkud přesnější vysvětlení uvádím v 7.6. Zde již ale vyžaduji jistou znalost z teorie kvadratických forem. Nezbytné minimum naleznete v 7.5.