

Next: 7.3 SLMS
Up: 7. Cvičení 7: Konvergenční
Previous: 7.1 LMS
Subsections
7.2 RLS
RLS algoritmus můžeme podobně jako LMS rozepsat do několika kroků.
Rovnice filtrace (4.1) je dána Obr. 4.1(a)
a zůstává bezezměny pouze ve shodě s užívaným značením pro RLS
posunu indexování u váhového vektoru
![\begin{displaymath}\begin{gathered}\hat{d}[n] = \mathbf{w}^T[n-1] \mathbf{x}[n] \\ e[n] = d[n] - \hat{d}[n] \end{gathered}\end{displaymath}](img365.png) |
(7.2) |
Rovnice úpravy vah
![$\displaystyle \mathbf{w}[n] = \mathbf{w}[n-1] - \mathbf{P}[n] \nabla_{\mathbf{w}[n-1]} e^2[n] = \mathbf{w}[n-1] + \mathbf{P}[n] \mu e[n] \mathbf{x}[n]$](img366.png) |
(7.3) |
se od LMS liší přenásobením záporně vzatého gradientu odhadem inverze
![$ \mathbf{P[n]}$](img367.png) autokorelační matice vstupního signálu
autokorelační matice vstupního signálu ![$ x[n]$](img1.png) . Přibývá
rovněž rovnice pro úpravu tohoto odhadu
. Přibývá
rovněž rovnice pro úpravu tohoto odhadu
![$\displaystyle \mathbf{P}[n] = \frac{1}{\beta} \left( \mathbf{P}[n-1] - \frac{\m...
...mathbf{P}[n-1]} {\beta + \mathbf{x}^T[n]\mathbf{P}[n-1]\mathbf{x}[n]} \right) .$](img368.png) |
(7.4) |
Abychom si vše ujasnili, nejprve si situaci trochu zjednoduššíme.
Předpokládejme, že známe autokorelační matici
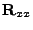 vstupního signálu. Rekurze pro odhad
vstupního signálu. Rekurze pro odhad
![$ \mathbf{P[n]}$](img367.png) tedy odpadá
a zbývá rovnice pro úpravu vah
tedy odpadá
a zbývá rovnice pro úpravu vah
Zavedl jsem navíc konstantu 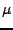 ovlivňující délku kroku.
Uplatněním operátoru střední hodnoty na (7.5) získáme rekurzi
pro střední hodnotu váhového
vektoru
ovlivňující délku kroku.
Uplatněním operátoru střední hodnoty na (7.5) získáme rekurzi
pro střední hodnotu váhového
vektoru
![$\displaystyle \mathrm{E}[\mathbf{w}[n]] = \mathrm{E}[\mathbf{w}[n-1]] + \mu \ma...
...n]d[n] ] - \mathrm{E}[ \mathbf{x}[n]\mathbf{x}^T[n] \mathbf{w}[n-1] ] \right) .$](img370.png) |
(7.6) |
Moment 3. řádu
![$ \mathrm{E}[\mathbf{x}[n]\mathbf{x}^T[n]\mathbf{w}[n-1]]$](img371.png) (
(
![$ \mathbf{w}[n-1]$](img372.png) je funkcí
je funkcí
![$ \mathbf{x}[n]$](img260.png) )
nám postup značně komplikuje. Zvolíme-li ale
)
nám postup značně komplikuje. Zvolíme-li ale 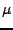 dostatečně malé
bude
dostatečně malé
bude
![$ \mathbf{w}[n-1]$](img372.png) záviset na
záviset na
![$ \mathbf{x}[n]$](img260.png) pouze minimálně,
takže oba náhodné vektory budeme moci považovat za nezávislé
(tzv. indepencence assumption). Uvedený moment 3. řádu pak
můžeme rozložit na součin dvou momentů a rovnice (7.6) pak přejde
na
pouze minimálně,
takže oba náhodné vektory budeme moci považovat za nezávislé
(tzv. indepencence assumption). Uvedený moment 3. řádu pak
můžeme rozložit na součin dvou momentů a rovnice (7.6) pak přejde
na
![$\displaystyle \mathrm{E}[\mathbf{w}[n]] = \mathrm{E}[\mathbf{w}[n-1]] + \mu \ma...
...left( \mathbf{r}_{xd} - \mathbf{R}_{xx} \mathrm{E}[ \mathbf{w}[n-1] ] \right) .$](img373.png) |
(7.7) |
kde
![$ \mathbf{R}_{xx} = \mathrm{E}[ \mathbf{x}[n] \mathbf{x}^T[n] ]$](img289.png) a
a
![$ \mathbf{r}_{xd} = \mathrm{E}[\mathbf{x}[n]d[n]]$](img374.png) .
Odečtením optimální hodnoty vah
.
Odečtením optimální hodnoty vah
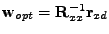 ,
kterou jste si odvodili pro úlohu predikce (2.9) (znaménko,
záměna
,
kterou jste si odvodili pro úlohu predikce (2.9) (znaménko,
záměna
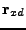 a
a
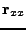 odpovídají změnám ve strukturě
prediktoru Obr. 2.3,Obr. 3.2 a estimátoru
Obr. 4.1(a)) od obou stran rovnosti (7.7) a
zavedením vektoru
odpovídají změnám ve strukturě
prediktoru Obr. 2.3,Obr. 3.2 a estimátoru
Obr. 4.1(a)) od obou stran rovnosti (7.7) a
zavedením vektoru
![$\displaystyle \mathbf{v}[n] = \mathrm{E}[\mathbf{w}[n]] - \mathbf{w}_{opt} ,$](img378.png) |
(7.8) |
dostáváme rovnici pro úpravu
![$ \mathbf{v}[n]$](img379.png)
Vidíme, že složky
![$ \mathbf{v}[n]$](img379.png) se s rostoucím časem
se s rostoucím časem
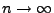 blíží k 0. Tedy z (7.8) se střední hodnota váhového vektoru
blíží
blíží k 0. Tedy z (7.8) se střední hodnota váhového vektoru
blíží
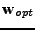 . Z (7.9) dále vidíme, že trajektorie
spojující
. Z (7.9) dále vidíme, že trajektorie
spojující
![$ \mathbf{v}[0]$](img383.png) a
a
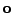 resp.
resp.
![$ \mathrm{E}[\mathbf{w}[0]]$](img384.png) a
a
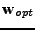 je úsečka, neboť všechny složky
je úsečka, neboť všechny složky
![$ \mathbf{v}[n]$](img379.png) se
blíží k 0 se stejnou časovou konstantou
se
blíží k 0 se stejnou časovou konstantou 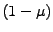 .
.
Cvičení 7.2: Buzení ![$ x[n]$](img1.png) modelujte jako barevné viz. cvičení 7.1,
a rozptyl aditivního šumu volte
modelujte jako barevné viz. cvičení 7.1,
a rozptyl aditivního šumu volte
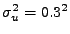 .
Implementujte RLS algoritmus s tím, že předpokládáme známou
autokorelační matici
.
Implementujte RLS algoritmus s tím, že předpokládáme známou
autokorelační matici
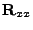 viz. (7.2) a (7.5).
Parametr
viz. (7.2) a (7.5).
Parametr 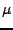 volte 1 (bez tlumení), 0.1, 0.01.
Porovnejte průběhy vah na čase a trajektore střední hodnoty
váhového vektoru ve váhovém prostoru.
volte 1 (bez tlumení), 0.1, 0.01.
Porovnejte průběhy vah na čase a trajektore střední hodnoty
váhového vektoru ve váhovém prostoru.
Výsledky:
Figure:
RLS - známá
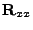 : Porovnání průběhů vah a
trajektorí váhového vektoru ve váhovém prostoru pro RLS (
: Porovnání průběhů vah a
trajektorí váhového vektoru ve váhovém prostoru pro RLS (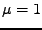 )
a RLS (
)
a RLS (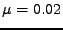 )
)
|
|
Nyní se trochu pokusím objasnit přesný význam
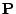 v rovnici
pro úpravu vah RLS algoritmu. Víme, že má vztah k autokorelační matici
v rovnici
pro úpravu vah RLS algoritmu. Víme, že má vztah k autokorelační matici
![$ \mathbf{R}_{xx} = \mathrm{E}[ \mathbf{x}[n] \mathbf{x}^T[n] ]$](img289.png) vstupního signálu.
Pro odhad střední hodnoty lze použít integrátoru
vstupního signálu.
Pro odhad střední hodnoty lze použít integrátoru
![$\displaystyle \mathbf{R}[n] = \beta \mathbf{R}[n-1] + \mathbf{x}[n]\mathbf{x}^T[n] .$](img388.png) |
(7.10) |
Uvedený integrátor je však nenormovaný
(u
![$ \mathbf{x}[n]\mathbf{x}^T[n]$](img389.png) chybí
chybí 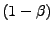 ) odhad (7.10)
trpí zesílením
) odhad (7.10)
trpí zesílením
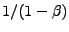 . Platí tedy
. Platí tedy
![$\displaystyle \mathbf{R}_{xx}[n] = (1-\beta)\mathbf{R}[n] .$](img392.png) |
(7.11) |
Z rovnice (7.10) lze obržet rekurzi pro
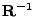 .
Ovození jsem umístil do 7.7 vyžaduje opět znalost
některých vlatsností
vlastního rozkladu symetrických matic, viz. 7.5.
.
Ovození jsem umístil do 7.7 vyžaduje opět znalost
některých vlatsností
vlastního rozkladu symetrických matic, viz. 7.5.
![\begin{displaymath}\begin{gathered}\mathbf{P}[n] = \frac{1}{\beta} \left( \mathb...
... \right) ,\\ \mathbf{P}[n] = \mathbf{R}^{-1}[n] ,\end{gathered}\end{displaymath}](img394.png) |
(7.12) |
kde jsem zavedl označení
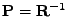 .
To je již původní rekurze (7.4).
Použitím (7.11) získáme vztah
mezi
.
To je již původní rekurze (7.4).
Použitím (7.11) získáme vztah
mezi
![$ \mathbf{R}_{xx}[n]$](img396.png) a
a
![$ \mathbf{P}[n]$](img397.png)
![$\displaystyle \mathbf{P}[n] = \mathbf{R}^{-1}[n] = (1-\beta)\mathbf{R}_{xx}^{-1}[n] .$](img398.png) |
(7.13) |
Vidíme, že
![$ \mathbf{P}[n]$](img397.png) není přímo
není přímo
![$ \mathbf{R}_{xx}^{-1}[n]$](img399.png) ,
ale liší se přidaným tlumením
,
ale liší se přidaným tlumením 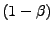 (v (7.5) označeno
jako
(v (7.5) označeno
jako 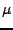 ).
).
Cvičení 7.3: Porovnejte průběhy vah na čase, trajektorie váhováho vektoru ve
váhovém prostoru pro LMS (
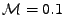 ) a RLS (
) a RLS (
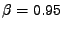 )
pro barevné buzení viz. cvičení 7.1.
)
pro barevné buzení viz. cvičení 7.1.
Výsledky:
Figure 7.4:
Porovnání průběhů vah a
trajektorí váhového vektoru ve váhovém prostoru pro RLS (
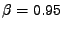 )
a LMS (
)
a LMS (
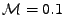 )
)
|
|
Figure 7.5:
Porovnání průběhů MSE pro RLS (
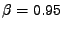 )
a LMS (
)
a LMS (
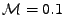 ) (všiměte si, že pouze průběh MSE pro LMS
se vyznačuje dvěma sklony)
) (všiměte si, že pouze průběh MSE pro LMS
se vyznačuje dvěma sklony)
|
|


Next: 7.3 SLMS
Up: 7. Cvičení 7: Konvergenční
Previous: 7.1 LMS
Mirek
2006-12-12
![]() modelujte jako barevné viz. cvičení 7.1,
a rozptyl aditivního šumu volte
modelujte jako barevné viz. cvičení 7.1,
a rozptyl aditivního šumu volte
![]() .
Implementujte RLS algoritmus s tím, že předpokládáme známou
autokorelační matici
.
Implementujte RLS algoritmus s tím, že předpokládáme známou
autokorelační matici
![]() viz. (7.2) a (7.5).
Parametr
viz. (7.2) a (7.5).
Parametr ![]() volte 1 (bez tlumení), 0.1, 0.01.
Porovnejte průběhy vah na čase a trajektore střední hodnoty
váhového vektoru ve váhovém prostoru.
volte 1 (bez tlumení), 0.1, 0.01.
Porovnejte průběhy vah na čase a trajektore střední hodnoty
váhového vektoru ve váhovém prostoru.
![\includegraphics[width=10cm]{ada7/obrmat/fig3.ps}](img386.png)
![]() ) a RLS (
) a RLS (
![]() )
pro barevné buzení viz. cvičení 7.1.
)
pro barevné buzení viz. cvičení 7.1.
![\includegraphics[width=10cm]{ada7/obrmat/fig4.ps}](img400.png)
![\includegraphics[width=10cm]{ada7/obrmat/fig5.ps}](img401.png)