

Next: 7.7 Odvození rekurze pro
Up: 7. Cvičení 7: Konvergenční
Previous: 7.5 Úvod do vlastního
7.6 Konvergence střední hodnoty váhového vektoru v LMS
Rovnice pro úpravu vah v LMS vypadá (identifikace)
Nyní provedu stejné úpravy jako v části o RLS 7.2.
Doporučuji tuto část přečíst předem. Rekurzi pro střední hodnotu váhového
vektoru
![$ \mathrm{E}[\mathbf{w}[n]]$](img363.png) získám uplatněním operátoru střední hodnoty na obě strany (7.50).
Vzniklý moment 3. řádu
získám uplatněním operátoru střední hodnoty na obě strany (7.50).
Vzniklý moment 3. řádu
![$ \mathrm{E}[\mathbf{x}[n] \mathbf{x}^T[n] \mathbf{w}[n]]$](img554.png) rozložím použitím předpokladu o nezávislosti
rozložím použitím předpokladu o nezávislosti
![$ \mathbf{x}[n]$](img260.png) a
a
![$ \mathbf{w}[n]$](img233.png) (dostatečně malé
(dostatečně malé 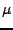 )
na součin dvou momentů
)
na součin dvou momentů
![$ \mathrm{E}[\mathbf{x}[n] \mathbf{x}^T[n]]$](img555.png) a
a
![$ \mathrm{E}[\mathbf{w}[n]]$](img363.png) .
Zavedu značení
.
Zavedu značení
![\begin{displaymath}\begin{gathered}\mathbf{R}_{xx} = \mathrm{E}[\mathbf{x}[n] \m...
...\mathbf{r}_{xd} = \mathrm{E}[\mathbf{x}[n]d[n]]. \end{gathered}\end{displaymath}](img556.png) |
(7.51) |
Od obou stran vzniklé rovnosti odečtu optimální hodnotu
váhového vektoru
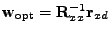 a zavedu vektor
a zavedu vektor
![$\displaystyle \mathbf{v}[n] = \mathrm{E}[\mathbf{w}[n]] - \mathbf{w}_{\mathrm{opt}} .$](img558.png) |
(7.52) |
Výsledná rovnost pak vypadá
Jelikož autokorelační matice
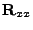 je reálná symetrická
existuje z lematu 7.5 její vlastní rozklad
je reálná symetrická
existuje z lematu 7.5 její vlastní rozklad
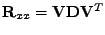 .
Dosadím do (7.53) a použiji ortogonalitu
.
Dosadím do (7.53) a použiji ortogonalitu
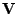
![$\displaystyle \mathbf{v}[n+1] = (\mathbf{E} - \mu \mathbf{V}\mathbf{D}\mathbf{V...
...hbf{v}[n] = \mathbf{V}(\mathbf{E} - \mu \mathbf{D})\mathbf{V}^T \mathbf{v}[n] .$](img561.png) |
(7.54) |
Zavedu vektor
![$\displaystyle \mathbf{u}[n] = \mathbf{V}^T \mathbf{v}[n] .$](img562.png) |
(7.55) |
Rovnost (7.54) vynásobím zleva
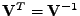 a dostanu
rekurzi pro
a dostanu
rekurzi pro
![$ \mathbf{u}[n]$](img564.png)
![$\displaystyle \mathbf{u}[n+1] = (\mathbf{E} - \mu \mathbf{D}) \mathbf{u}[n] .$](img565.png) |
(7.56) |
Z lemmatu 7.5 má
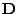 tvar
tvar
![$ \mathbf{D} = \mathrm{diag}([\lambda_1,\ldots,\lambda_N])$](img517.png) ,
kde
,
kde
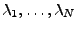 jsou všechna vlastní čísla
jsou všechna vlastní čísla
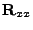 včetně násoností. Mohu tedy (7.56)
rozepsat jednoduše
pro jednotlivé složky
včetně násoností. Mohu tedy (7.56)
rozepsat jednoduše
pro jednotlivé složky
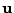
![$\displaystyle u_k[n] = (1-\mu\lambda_k)^n u_k[0], \;\;\;\; k = 1,\ldots,N .$](img567.png) |
(7.57) |
Aby konvergovaly pro
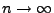
![$ u_k[n]$](img568.png) k nule,
z (7.55)
k nule,
z (7.55)
![$ \mathbf{v}[n]$](img379.png) k
k
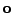 a z (7.52)
a z (7.52)
![$ \mathrm{E}[\mathbf{w}[n]]$](img363.png) k
k
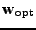 , musí být z (7.57)
nutně všechna vlastní
čísla
, musí být z (7.57)
nutně všechna vlastní
čísla
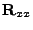 ostře větší než 0 (
ostře větší než 0 (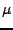 je kladná konstanta),
což je splněno
pro regulární
je kladná konstanta),
což je splněno
pro regulární
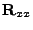 , viz. (7.48)
a současně musí platit
, viz. (7.48)
a současně musí platit
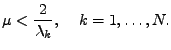 |
(7.58) |
Nejrestriktivnější z pohledu na horní mez pro 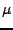 (7.58)
je největší vlastní číslo. Proto postačuje
(7.58)
je největší vlastní číslo. Proto postačuje
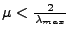 , které můžeme pro stacionárního náhodný
proces
, které můžeme pro stacionárního náhodný
proces ![$ x[n]$](img1.png) shora omezit podle (7.49).
Horní mez pro
shora omezit podle (7.49).
Horní mez pro 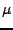 se pak
zjednodušší na
se pak
zjednodušší na
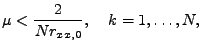 |
(7.59) |
což už se trochu podobá námi užívané horní mezi (7.1), která je ale
stále o něco restriktivnější. Je to dáno tím, že nepostačuje,
konverguje-li vektor vah pouze ve střední hodnotě k optimu, musí
konvergovat i ve varianci (k nule). Z analýzy konvergence ve varianci
právě vyplyne námi používaná horní mez (7.1).
Dále si všiměte, že z (7.57) jde střední hodnota váhového
vektoru k optimu po přímce pouze pro shodná vlastní čísla (tedy pokud
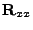 má jedno vlastní číslo násobnosti
má jedno vlastní číslo násobnosti 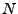 ). To ale platí
pouze pro bílé stacionární náhodné procesy. Pro barevné (různá
vlastní čísla) se průběh střední hodnoty váhového vektoru může
od přímky značně odlišovat. Např. díky různým vlastním číslům může
v jedné složce vektoru
). To ale platí
pouze pro bílé stacionární náhodné procesy. Pro barevné (různá
vlastní čísla) se průběh střední hodnoty váhového vektoru může
od přímky značně odlišovat. Např. díky různým vlastním číslům může
v jedné složce vektoru
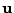 zkovergovat velice rychle a v jiné
velice pomalu, jak jste ostatně již pozorovali.
zkovergovat velice rychle a v jiné
velice pomalu, jak jste ostatně již pozorovali.


Next: 7.7 Odvození rekurze pro
Up: 7. Cvičení 7: Konvergenční
Previous: 7.5 Úvod do vlastního
Mirek
2006-12-12
![\begin{equation*}\begin{aligned}\mathbf{w}[n+1] &= \mathbf{w}[n] + \mu \mathbf{x...
...] - \mathbf{x}[n] \mathbf{x}^T[n] \mathbf{w}[n] ) . \end{aligned}\end{equation*}](img553.png)
![]() má jedno vlastní číslo násobnosti
má jedno vlastní číslo násobnosti ![]() ). To ale platí
pouze pro bílé stacionární náhodné procesy. Pro barevné (různá
vlastní čísla) se průběh střední hodnoty váhového vektoru může
od přímky značně odlišovat. Např. díky různým vlastním číslům může
v jedné složce vektoru
). To ale platí
pouze pro bílé stacionární náhodné procesy. Pro barevné (různá
vlastní čísla) se průběh střední hodnoty váhového vektoru může
od přímky značně odlišovat. Např. díky různým vlastním číslům může
v jedné složce vektoru
![]() zkovergovat velice rychle a v jiné
velice pomalu, jak jste ostatně již pozorovali.
zkovergovat velice rychle a v jiné
velice pomalu, jak jste ostatně již pozorovali.