

Next: 8.2 Kaskáda IIR prediktorů
Up: 8. Cvičení 8: Odhad
Previous: 8. Cvičení 8: Odhad
Ve 3. cvičení jsme již prediktor 2. řádu použili na odhad
frekvence harmonického signálu.
V tomto cvičení se budeme zbývat obecnější úlohou.
Jak postupovat je-li ve vstupním signálu přítomo více harmonických
složek?
Mohli bychom zachovat transverzální strukturu Obr. 3.2 a
pouze zvýšit řád podle toho kolik frekvencí bychom chtěli odhadnout.
Problém pak ale nastává při přepočtu hodnot vah
na odhady frekvencí (úhly nul filtru), který vyžaduje výpočet kořenů
polynomu stupně vyššího než dva (už při stupni 5 neumím řešit pomocí
odmocnin).
Jedna možnost jak se této komplikaci vyhnout (a tak významě snížit
složitost) je použití kaskády filtrů druhého řádu.
Nuly celé kaskády jsou pak totiž nulami jednotlivých filtrů druhého řádu
a lze je tedy jednoduše určit. Ve 3. cvičení jsem podrobně rozebral
vztah vah prediktoru 2. řádu Obr. 3.2
k modulu a úhlům (komplexně sdružených) nul
jeho přenosové funkce (za předpokladu pomalé změny vah) viz. (3.6)
(
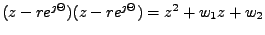 )
)
Zde navíc prediktor ještě zjednodušším. Omezím možné polohy nul na
jednotkovou kružnici (jejich modul 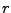 fixuji na 1), takže
fixuji na 1), takže
![$ w_2[n]=r^2 = 1$](img601.png) je
fixována a zbýva upravovat pouze Jedinou váhu. Místo označení
je
fixována a zbýva upravovat pouze Jedinou váhu. Místo označení ![$ w_1[n]$](img283.png) zde budu používat názornějšího značení
zde budu používat názornějšího značení
![$\displaystyle c[n] = -\frac{w_1[n]}{2} = \cos(\Theta)$](img602.png) |
(8.1) |
mající význam kosinu úhlu nuly.
V tomto cvičení se omezím pouze na odhad dvou frekvencí
(zobecnění na více je přímočaré). K tomu použijeme kaskádu dvou
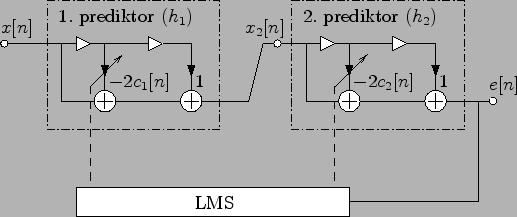
prediktorů 2. řádu viz. Obr. 8.1.
Figure 8.1:
Kaskáda FIR prediktorů 2. řádu pro odhad dvou frekvencí
 |
Vztah vah 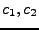 a odhadovaných frekvencí je z (8.1)
a odhadovaných frekvencí je z (8.1)
Z Obr. 8.1 jednoduše napíšeme rovnice filtrace (1. a 2. prediktor)
Abychom mohli sestavit rovnice pro úpravu vah potřebujeme nejprve
určit derivace
![$ \frac{\partial e[n]}{\partial c_1[n]}$](img607.png) ,
,
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) potřebné pro
zapsání gradientu účelové funkce
potřebné pro
zapsání gradientu účelové funkce ![$ e^2[n]$](img169.png) . S derivací
. S derivací
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) není problém
není problém
![$\displaystyle \frac{\partial e[n]}{\partial c_2[n]} = - 2 x_2[n-1] .$](img609.png) |
(8.4) |
Případ
![$ \frac{\partial e[n]}{\partial c_1[n]}$](img607.png) je trochu komplikovanější
neboť 1. prediktor je již dále od chybového výstupu
je trochu komplikovanější
neboť 1. prediktor je již dále od chybového výstupu ![$ e[n]$](img13.png) . Zde ještě
samozřejmě můžeme do rovnice pro
. Zde ještě
samozřejmě můžeme do rovnice pro ![$ e[n]$](img13.png) (8.3) dosadit za
(8.3) dosadit za ![$ x_2[n]$](img610.png) ,
ale všiměme si, že členů přibývá. Pro kaskádu IIR 2. řádu toto řešení
dokonce aplikovat nelze.
V LTI přiblížení8.1mohu ale oba prediktory prohodit aniž by se změnila impulsová odezva
celé kaskády
8.2jak je znázorněno na Obr. 8.2 a tak připojit 1. prediktor přímo k
chybovému výstupu
,
ale všiměme si, že členů přibývá. Pro kaskádu IIR 2. řádu toto řešení
dokonce aplikovat nelze.
V LTI přiblížení8.1mohu ale oba prediktory prohodit aniž by se změnila impulsová odezva
celé kaskády
8.2jak je znázorněno na Obr. 8.2 a tak připojit 1. prediktor přímo k
chybovému výstupu ![$ e[n]$](img13.png) .
.
Figure 8.2:
V LTI přiblížení mohu oba prediktory prohodit
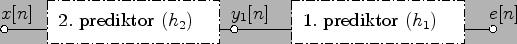 |
Pro Obr. 8.2 jednoduše sestavím rovnice filtrace
a již jednoduše určím problematickou derivaci
![$\displaystyle \frac{\partial e[n]}{\partial c_1[n]} = - 2 y_1[n-1] .$](img615.png) |
(8.6) |
Všechno kromě ![$ y_1[n]$](img616.png) je již vypočteno v (8.3). Pro výpočet
je již vypočteno v (8.3). Pro výpočet
![$ y_1[n]$](img616.png) použijeme (8.5). Celá struktura je znázorněna na
Obr. 8.3.
použijeme (8.5). Celá struktura je znázorněna na
Obr. 8.3.
Figure 8.3:
Celá struktura
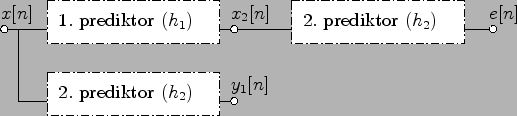 |
S použitím (8.6) a (8.4)
již jednoduše napíšeme rovnice
pro úpravu vah
Cvičení 8.0: Vstupní signál ![$ x[n]$](img1.png) modelujte jako směs dvou harmonických signálů
o jednotkových efektivních hodnotách a
frekvencích
modelujte jako směs dvou harmonických signálů
o jednotkových efektivních hodnotách a
frekvencích 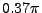 a
a 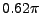 [rad/vzorek].
Délku
[rad/vzorek].
Délku ![$ x[n]$](img1.png) volte
volte 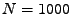 vzorků.
vzorků.
Napište skript v Matlabu implementující strukturu Obr. 8.1.
Konvergenční konstantu 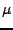 volte mu = 0.003/rxx0.
Počáteční podmínku pro
volte mu = 0.003/rxx0.
Počáteční podmínku pro ![$ c_1[n]$](img622.png) volte
volte
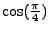 a
pro počáteční podmínku pro
a
pro počáteční podmínku pro ![$ c_2[n]$](img624.png) volte
volte
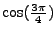 .
.
Vyneste odhady frekvencí na čase a porovnejte je se skutečnými frekvencemi.
Dále charakteristiku filtru v ustáleném stavu, a amplitudová spektra
vstupního signálu ![$ x[n]$](img1.png) a chybového výstupu
a chybového výstupu ![$ e[n]$](img13.png) .
.
Výsledky:
Figure 8.4:
Kaskáda FIR, žádné aditiví rušení: Spektrogram vstupu ![$ x[n]$](img1.png) , výstupu
, výstupu ![$ e[n]$](img13.png) ,
průběh vah na čase.
,
průběh vah na čase.
|
|
Figure 8.5:
Kaskáda FIR, žádné aditiví rušení: (zleva doprava)
amplitudová spektra vstupu ![$ x[n]$](img1.png) a výstupu
a výstupu ![$ e[n]$](img13.png) ,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
|
|
Cvičení 8.1: K vstupnímu signálu ![$ x[n]$](img1.png) navíc oproti předešlému cvičení 8.1
přičtěte
aditivní rušení
navíc oproti předešlému cvičení 8.1
přičtěte
aditivní rušení ![$ u[n]$](img14.png) .
Aditivní rušení
.
Aditivní rušení ![$ u[n]$](img14.png) modelujte jako bílý stacionární
gausovský proces s nulovou střední hodnotou.
Varianci šumu volte nejdříve
modelujte jako bílý stacionární
gausovský proces s nulovou střední hodnotou.
Varianci šumu volte nejdříve
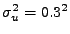 a pak
a pak
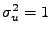 .
Vyneste si opět grafy jako ve cvičení 8.1
a pozorujte rozdíly.
.
Vyneste si opět grafy jako ve cvičení 8.1
a pozorujte rozdíly.
Výsledky:
Figure 8.6:
Kaskáda FIR, rozptyl adidivního rušení
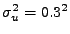 : (zleva doprava)
amplitudová spektra vstupu
: (zleva doprava)
amplitudová spektra vstupu ![$ x[n]$](img1.png) a výstupu
a výstupu ![$ e[n]$](img13.png) ,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
|
|
Figure 8.7:
Kaskáda FIR, rozptyl adidivního rušení
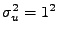 : (zleva doprava)
amplitudová spektra vstupu
: (zleva doprava)
amplitudová spektra vstupu ![$ x[n]$](img1.png) a výstupu
a výstupu ![$ e[n]$](img13.png) ,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
|
|


Next: 8.2 Kaskáda IIR prediktorů
Up: 8. Cvičení 8: Odhad
Previous: 8. Cvičení 8: Odhad
Mirek
2006-12-12
![]() )
)
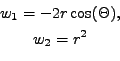
![]() a odhadovaných frekvencí je z (8.1)
a odhadovaných frekvencí je z (8.1)
![]() modelujte jako směs dvou harmonických signálů
o jednotkových efektivních hodnotách a
frekvencích
modelujte jako směs dvou harmonických signálů
o jednotkových efektivních hodnotách a
frekvencích ![]() a
a ![]() [rad/vzorek].
Délku
[rad/vzorek].
Délku ![]() volte
volte ![]() vzorků.
vzorků.
![]() volte mu = 0.003/rxx0.
Počáteční podmínku pro
volte mu = 0.003/rxx0.
Počáteční podmínku pro ![]() volte
volte
![]() a
pro počáteční podmínku pro
a
pro počáteční podmínku pro ![]() volte
volte
![]() .
.
![]() a chybového výstupu
a chybového výstupu ![]() .
.
![\includegraphics[width=10cm]{ada8/obrmat/fig2.ps}](img627.png)
![]() navíc oproti předešlému cvičení 8.1
přičtěte
aditivní rušení
navíc oproti předešlému cvičení 8.1
přičtěte
aditivní rušení ![]() .
Aditivní rušení
.
Aditivní rušení ![]() modelujte jako bílý stacionární
gausovský proces s nulovou střední hodnotou.
Varianci šumu volte nejdříve
modelujte jako bílý stacionární
gausovský proces s nulovou střední hodnotou.
Varianci šumu volte nejdříve
![]() a pak
a pak
![]() .
Vyneste si opět grafy jako ve cvičení 8.1
a pozorujte rozdíly.
.
Vyneste si opět grafy jako ve cvičení 8.1
a pozorujte rozdíly.
![\includegraphics[width=10cm]{ada8/obrmat/fig3.ps}](img628.png)
![\includegraphics[width=10cm]{ada8/obrmat/fig4.ps}](img629.png)