

Next: 9. Cvičení 9: Adaptive
Up: 8. Cvičení 8: Odhad
Previous: 8.1 Kaskáda FIR prediktorů
Charakteristika prediktorů 2. řádu není příliš selektivní.
Velké zlepšení z hlediska selektivity lze dosáhnout umístěním komplexně
sdružených pólů v úhlech nul původního filtru poblíž jednotkové kružnice.
Přenosová funkce výsledného systému má pak tvar
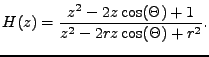 |
(8.8) |
V čitateli vidíme dvě komplexně sdružené nuly
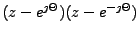 a ve jmenovateli
dva komplexně sdružené póly
a ve jmenovateli
dva komplexně sdružené póly
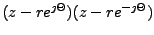 na stejných
úhlech
na stejných
úhlech 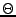 ,
,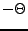 s modulem
s modulem 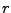 .
Na Obr. 8.8
je vidět srovnání systémů s přenosovou funkcí (8.8)
pro různé moduly pólů.
.
Na Obr. 8.8
je vidět srovnání systémů s přenosovou funkcí (8.8)
pro různé moduly pólů.
Figure 8.8:
Porovnání frekvenčních charakteristik systémů s přenosovou funkcí
(8.8) pro různé volby 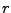 (jsou vyneseny i polohy nul a pólů)
(jsou vyneseny i polohy nul a pólů)
|
|
Modul pólů 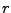 (ovlivňuje selektivitu) budu voli fixní.
Jediná věc, která lze upravovat je opět pouze úhel nuly
(ovlivňuje selektivitu) budu voli fixní.
Jediná věc, která lze upravovat je opět pouze úhel nuly 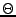 případně
případně
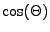 . Váhy zavedu tedy shodně s (8.2).
Z přenosové fce (8.8) jednoduše přejdeme ke struktuře.
Kaskáda IIR prediktorů 2. řádu je na Obr. 8.9.
. Váhy zavedu tedy shodně s (8.2).
Z přenosové fce (8.8) jednoduše přejdeme ke struktuře.
Kaskáda IIR prediktorů 2. řádu je na Obr. 8.9.
Figure 8.9:
Kaskáda IIR prediktorů 2. řádu pro odhad dvou frekvencí
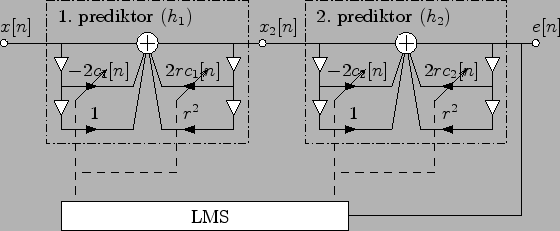 |
Z Obr. 8.9 jednoduše sesvíme rovnice filtrace
(oproti (8.3) přibydou zpětné vazby)
K tomu, abychom sestavili rovnice pro úpravu ![$ c_1[n]$](img622.png) a
a ![$ c_2[n]$](img624.png) potřebujeme opět určit derivace
potřebujeme opět určit derivace
![$ \frac{\partial e[n]}{\partial c_1[n]}$](img607.png) ,
,
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) .
Opět začneme s
.
Opět začneme s
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) .
Zpětnou vazbou se situace značně komplikuje, ale za předpokladu,
že
.
Zpětnou vazbou se situace značně komplikuje, ale za předpokladu,
že ![$ c_2[n]$](img624.png) ,
, ![$ c_2[n-1]$](img638.png) a
a ![$ c_2[n-2]$](img639.png) lze považovat za přibližně
shodné
lze považovat za přibližně
shodné
![$ c_2[n] = c_2[n-1] = c_2[n-2]$](img640.png) (dostatečně malé
(dostatečně malé 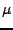 )
dospějeme k rekurzivnímu vztahu pro
)
dospějeme k rekurzivnímu vztahu pro
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) (
(
![$ \frac{\partial e[n]}{\partial c_2[n]}$](img608.png) označím
označím ![$ d_2[n]$](img641.png) )
)
![$\displaystyle \frac{\partial e[n]}{\partial c_2[n]} = d_2[n] = - 2 x_2[n-1] + 2 r e[n-1] + 2 r c_2[n] d_2[n-1] - r^2 d_2[n-2] .$](img642.png) |
(8.10) |
Derivaci
![$ \frac{\partial e[n]}{\partial c_1[n]}$](img607.png) stanovíme opět
s použitím LTI předpokladu. Prohodíme opět oba prediktory jako na
Obr. 8.2
a napíšeme rovnice filtrace
stanovíme opět
s použitím LTI předpokladu. Prohodíme opět oba prediktory jako na
Obr. 8.2
a napíšeme rovnice filtrace
a již obdobně jako v (8.10) (předpoklad pomalu měnících se vah)
určím problematickou derivaci
![$\displaystyle \frac{\partial e[n]}{\partial c_1[n]} = d_1[n] = - 2 y_1[n-1] + 2 r e[n-1] + 2 r c_1[n] d_1[n-1] - r^2 d_1[n-2] .$](img644.png) |
(8.12) |
Obrázek výsledné struktury lze opět převzít, viz. Obr. 8.3.
S použitím (8.12) a (8.10)
již jednoduše sestavíme rovnice pro
úpravu vah
Cvičení 8.2: Vystupní signál ![$ x[n]$](img1.png) modelujte shodně jako ve cvičení 8.1.
Napište skript v Matlabu implementující strukturu Obr. 8.9
(kaskádu IIR prediktorů 2. řádu pro odhad dvou frekvencí)
Porovnejte výsledky (odhady frekvencí na čase, atd.)
oproti výsledkům získaným ve cvičení 8.1
(kaskádu FIR prediktorů 2. řádu pro odhad dvou frekvencí).
modelujte shodně jako ve cvičení 8.1.
Napište skript v Matlabu implementující strukturu Obr. 8.9
(kaskádu IIR prediktorů 2. řádu pro odhad dvou frekvencí)
Porovnejte výsledky (odhady frekvencí na čase, atd.)
oproti výsledkům získaným ve cvičení 8.1
(kaskádu FIR prediktorů 2. řádu pro odhad dvou frekvencí).
Výsledky:
Figure 8.10:
Kaskáda IIR, rozptyl adidivního rušení
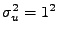 : (zleva doprava)
amplitudová spektra vstupu
: (zleva doprava)
amplitudová spektra vstupu ![$ x[n]$](img1.png) a výstupu
a výstupu ![$ e[n]$](img13.png) ,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
,
průběh odhadu frekvencí na čase, modulové frekvenční charakteristiky
kaskády a obou prediktorů 2. řádu, polohy nul a pólů přenosové funkce
kaskády v z-rovině.
|
|


Next: 9. Cvičení 9: Adaptive
Up: 8. Cvičení 8: Odhad
Previous: 8.1 Kaskáda FIR prediktorů
Mirek
2006-12-12
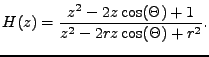
![\includegraphics[width=10cm]{ada8/obrmat/fig10.ps}](img634.png)
![]() (ovlivňuje selektivitu) budu voli fixní.
Jediná věc, která lze upravovat je opět pouze úhel nuly
(ovlivňuje selektivitu) budu voli fixní.
Jediná věc, která lze upravovat je opět pouze úhel nuly ![]() případně
případně
![]() . Váhy zavedu tedy shodně s (8.2).
Z přenosové fce (8.8) jednoduše přejdeme ke struktuře.
Kaskáda IIR prediktorů 2. řádu je na Obr. 8.9.
. Váhy zavedu tedy shodně s (8.2).
Z přenosové fce (8.8) jednoduše přejdeme ke struktuře.
Kaskáda IIR prediktorů 2. řádu je na Obr. 8.9.
![]() modelujte shodně jako ve cvičení 8.1.
Napište skript v Matlabu implementující strukturu Obr. 8.9
(kaskádu IIR prediktorů 2. řádu pro odhad dvou frekvencí)
Porovnejte výsledky (odhady frekvencí na čase, atd.)
oproti výsledkům získaným ve cvičení 8.1
(kaskádu FIR prediktorů 2. řádu pro odhad dvou frekvencí).
modelujte shodně jako ve cvičení 8.1.
Napište skript v Matlabu implementující strukturu Obr. 8.9
(kaskádu IIR prediktorů 2. řádu pro odhad dvou frekvencí)
Porovnejte výsledky (odhady frekvencí na čase, atd.)
oproti výsledkům získaným ve cvičení 8.1
(kaskádu FIR prediktorů 2. řádu pro odhad dvou frekvencí).
![\includegraphics[width=10cm]{ada8/obrmat/fig5.ps}](img646.png)