

Next: 11.1 Statistiky vyšších řádů
Up: Cvičení k předmětu ADA
Previous: 10. Cvičení 10: Separace
Shrňme nejprve závěry z minulého cvičení věnovanému separaci
pomocí statistik 2. řádů.
Máme k dispozici směs nezávislých procesů.
Směs je reprezentována náhodným vektorem
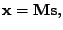 |
(11.1) |
kde
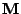 je jakákoli regulární matice (mixážní matice) a
náhodný vektor
je jakákoli regulární matice (mixážní matice) a
náhodný vektor
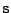 s nezávislými složkami reprezentuje
ony nezávislé procesy.
s nezávislými složkami reprezentuje
ony nezávislé procesy.
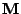 i
i
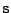 nejsou známy.
Naším cílem je najít transformaci (separační matici), která ze směsi
obnoví původní nezávislé procesy (s pomocí reprezentujících náhodných
vektorů: která z
nejsou známy.
Naším cílem je najít transformaci (separační matici), která ze směsi
obnoví původní nezávislé procesy (s pomocí reprezentujících náhodných
vektorů: která z
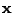 separuje původní složky
separuje původní složky
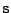 ).
Používáme k tomu nezávislost složek
).
Používáme k tomu nezávislost složek
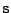 .
Hledáme tedy transformaci, která transformuje
.
Hledáme tedy transformaci, která transformuje
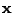 na
náhodný vektor s nezávislými složkami. To že nalezená transformace
skutečně separuje původní složky
na
náhodný vektor s nezávislými složkami. To že nalezená transformace
skutečně separuje původní složky
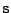 nemusí být pravda
viz. příklad s normálními rozděleními viz. Obr. 10.5, ale je-li
transformace nezávislostí složek výsledku určena jednoznačně, až na
permutaci a měřítka složek
11.1, pak musí separovat původní složky
nemusí být pravda
viz. příklad s normálními rozděleními viz. Obr. 10.5, ale je-li
transformace nezávislostí složek výsledku určena jednoznačně, až na
permutaci a měřítka složek
11.1, pak musí separovat původní složky
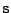 (
(
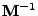 má také uvedené vlastnosti, tak to musí být z jednoznačnosti ona,
až na permutci a měřítka).
má také uvedené vlastnosti, tak to musí být z jednoznačnosti ona,
až na permutci a měřítka).
Označme
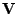 ortogonální matici a
ortogonální matici a
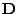 diagonální matici
vlastního rozkladu korelační matice
diagonální matici
vlastního rozkladu korelační matice
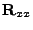
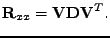 |
(11.2) |
Bylo ukázáno, že transformace
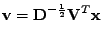 |
(11.3) |
složky
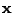 vždy dekoreluje, což lze nahlédnout výpočtem
korelační matice výsledku
vždy dekoreluje, což lze nahlédnout výpočtem
korelační matice výsledku
![$\displaystyle \mathbf{R}_{vv} = \mathrm{E}[\mathbf{v}\mathbf{v}^T] = \mathbf{D}...
...hbf{V}\mathbf{D}\mathbf{V}^T \mathbf{V}\mathbf{D}^{-\frac{1}{2}} = \mathbf{E} .$](img757.png) |
(11.4) |
To samozřejmě ještě neznamená, že
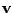 musí mít nezávislé složky.
Zbývá tedy najít transformaci (matici)
musí mít nezávislé složky.
Zbývá tedy najít transformaci (matici)
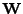
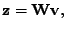 |
(11.5) |
která transformuje
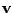 na vektor s nezávislými složkami (označen
na vektor s nezávislými složkami (označen
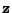 ).
Z nezávislosti složek
).
Z nezávislosti složek
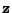 plyne jejich nekorelovanost (změny
měřítek mě opět nezajímají, proto se místo diagonální omezuji opět na
jednotkovou korelační matici)
plyne jejich nekorelovanost (změny
měřítek mě opět nezajímají, proto se místo diagonální omezuji opět na
jednotkovou korelační matici)
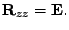 |
(11.6) |
Korelační matici můžeme vyjádřit rovněž pomocí (11.5) a
(11.4)
![$\displaystyle \mathbf{R}_{zz} = \mathrm{E}[\mathbf{z}\mathbf{z}^T] = \mathbf{W}...
..._{vv}\mathbf{W}^T = \mathbf{W}\mathbf{E}\mathbf{W}^T = \mathbf{W}\mathbf{W}^T .$](img761.png) |
(11.7) |
Z (11.6) a (11.7)
dostáváme omezující podmínku na možné
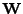
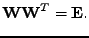 |
(11.8) |
Hledaná matice
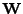 tedy musí být ortogonální.
Dekorelace (vybělení) složek
tedy musí být ortogonální.
Dekorelace (vybělení) složek
 tedy nevede obecně k separaci,
ale úlohu značně zjednodušší (při hledání vhodné matice
tedy nevede obecně k separaci,
ale úlohu značně zjednodušší (při hledání vhodné matice
 nemusíme vybírat mezi všemi regulárními maticemi, ale stačí se soustředit
na ortogonální matice).
nemusíme vybírat mezi všemi regulárními maticemi, ale stačí se soustředit
na ortogonální matice).
Subsections


Next: 11.1 Statistiky vyšších řádů
Up: Cvičení k předmětu ADA
Previous: 10. Cvičení 10: Separace
Mirek
2006-12-12
![]()
![]() ortogonální matici a
ortogonální matici a
![]() diagonální matici
vlastního rozkladu korelační matice
diagonální matici
vlastního rozkladu korelační matice
![]()
![]() musí mít nezávislé složky.
Zbývá tedy najít transformaci (matici)
musí mít nezávislé složky.
Zbývá tedy najít transformaci (matici)
![]()