

Next: 12. Cvičení 12: Směrový
Up: 11. Cvičení 11: Dokončení
Previous: 11. Cvičení 11: Dokončení
Subsections
Je zřejmé, že pomocí statistik 2. řádů hledané
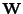 nenajdeme
(pro jakékoli ortogonální
nenajdeme
(pro jakékoli ortogonální
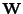 jsou složky
jsou složky
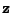 dekorelované).
Musíme tedy sáhnout po statistikách vyšších řádů.
dekorelované).
Musíme tedy sáhnout po statistikách vyšších řádů.
Nejprve se podíváme na momenty.
Momenty můžeme charakterizovat jako koeficienty Taylorova rozvoje
charakteristické funkce (v
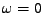 ).
Mějme náhodnou veličinu
).
Mějme náhodnou veličinu 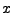 její hustotu
pravděpodobnosti označíme
její hustotu
pravděpodobnosti označíme  a charakteristickou funkci
a charakteristickou funkci
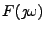 (Fourierovu transformaci
(Fourierovu transformaci 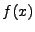 )
)
![$\displaystyle F(\jmath \omega) = \mathrm{E}[e^{\jmath \omega x}] = \intop_{\mat...
...}(0) (\jmath \omega)^k = \sum_{k=0}^{\infty} \frac{m_k}{k!} (\jmath \omega)^k .$](img765.png) |
(11.9) |
První a druhá rovnost je vyjádření charakteristické funkce pomocí
Furierovy transformace z hustoty pravděpodobnosti. První vyjádření
je zapsáno pomocí operátoru střední hodnoty. Třetí a čtvrtá rovnost
je vyjádření charakteristické funkce pomocí Taylorova rozvoje.
Pro momenty jsem použil zkráceného označení
![$ m_k = \mathrm{E}[x^k]$](img766.png) (budu ho používat jeli zřejmé o jakou hustotu
příadně náhodnou veličinu se jedná, v opačném případě budu
používat přesnějších označení:
(budu ho používat jeli zřejmé o jakou hustotu
příadně náhodnou veličinu se jedná, v opačném případě budu
používat přesnějších označení: 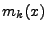 -
- 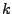 -tý moment pro náhodnou veličinu
-tý moment pro náhodnou veličinu
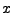 ,
, 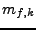 -
- 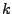 -tý moment pro hustotu
-tý moment pro hustotu 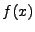 ).
Poslední rovnost říká, že momenty jsou derivacemi charakteristické
funkce v nule. To můžeme jednoduše ukázat
11.2
).
Poslední rovnost říká, že momenty jsou derivacemi charakteristické
funkce v nule. To můžeme jednoduše ukázat
11.2
Složky směsi
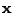 lze z (11.1)
lze rozepsat jako lineární kombinace
nezávislých náhodných veličin. Hledání
lze z (11.1)
lze rozepsat jako lineární kombinace
nezávislých náhodných veličin. Hledání
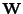 znamená vlastně nalézt
koeficienty lineárních kombinací. Proto nás zajímá, zda se tyto operace
dají pomocí momentů jednoduše vyjádřit.
Lineární kombinaci
nezávislých náhodných veličin mohu vždy rozepsat pomocí součtu nezávislých
náhodných veličin a skalárního násobku.
Co se při těchto operacích děje s momenty?
Jelikož známe vztah charakteristické funkce a momentů je odpověď
jednoduchá.
znamená vlastně nalézt
koeficienty lineárních kombinací. Proto nás zajímá, zda se tyto operace
dají pomocí momentů jednoduše vyjádřit.
Lineární kombinaci
nezávislých náhodných veličin mohu vždy rozepsat pomocí součtu nezávislých
náhodných veličin a skalárního násobku.
Co se při těchto operacích děje s momenty?
Jelikož známe vztah charakteristické funkce a momentů je odpověď
jednoduchá.
Nejprve se podíváme na součet.
Mějme dvě nezávislé náhodné veličiny 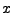 a
a 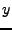 , jejich součet označíme
, jejich součet označíme
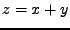 . Hustoty pravděpodobnosti označím
. Hustoty pravděpodobnosti označím
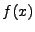 ,
, 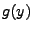 a
a 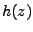 . Charakteristické funkce označím velkými písmeny
jak jsme zvyklí u obrazů Fourierovy transformace
. Charakteristické funkce označím velkými písmeny
jak jsme zvyklí u obrazů Fourierovy transformace
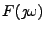 ,
,
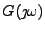 ,
,
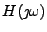 . Tabulka 11.1 uvádí
co se děje s hustotami, charakteristickými funkcemi, atd. při
součtu nezávislých náhodných veličin.
. Tabulka 11.1 uvádí
co se děje s hustotami, charakteristickými funkcemi, atd. při
součtu nezávislých náhodných veličin.
Table 11.1:
Součet nezávislých náhodných veličin
| hustoty pravděpodobnosti |
charakteristické funkce |
logaritmy char. funkcí |
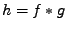 |
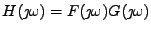 |
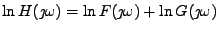 |
|
Jak víte hustota součtu nezávislých náhodných veličin vede na konvoluci
hustot sčítanců
což je první sloupec tabulky. Víte také, že Furierovy obrazy se při konvoluci
předmětů násobí, to je druhý sloupec (charakteristické funkce jsou Fourierovy
obrazy hustot). Jak je to s momenty se dozvíme, rozepíšeme-li druhý sloupec
tabulky pomocí Taylorových rozvojů
Vidíme, že se jedná o součin dvou polynomů. Všiměte si, že při výpočtu
koeficientů součinu polynomů konvolvujete koeficienty sčítanců.
Momenty součtu jsou tedy dány konvolucí momentů sčítanců.
To je již docela složitý vztah. Proto se raději budeme snažit nalézt
jiné charakteristiky ve kterých by se součet náhodných veličin
vyjadřoval snadněji.
Postupujeme obdobně jako v kepstrální analýze, místo charakteristických
funkcí budeme pracovat s jejich logaritmy, viz. 4. sloupec tabulky
(součin přejde v logaritmu na součet). Místo momentů
(derivací charakteristické funkce v nule) vezmeme derivace logarimu
charakteristické funkce v nule.
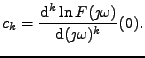 |
(11.11) |
Jedná se tedy o koeficienty Taylorova rozvoje logaritmu charakteristické
funkce
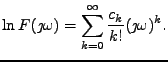 |
(11.12) |
Tyto charakteristiky
se nazývají kumulanty. Zavedu značení 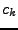 pro
pro 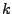 -tý kumulant
(případně
-tý kumulant
(případně 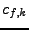 nebo
nebo 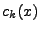 ).
Zpíšemi-li nyní 4. slopec tabulky pomocí Taylorových rozvojů
).
Zpíšemi-li nyní 4. slopec tabulky pomocí Taylorových rozvojů
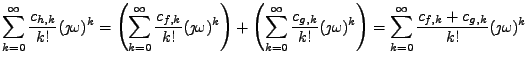 |
(11.13) |
zjistíme, že se kumulanty jednoduše sčítají. Toto vlastnost jsem
poněkud čitelněji zapsal do tabulky 11.2
Table 11.2:
Vlastnosti kumulantů (předpokládáme, že 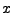 a
a 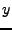 jsou
nezávislé náhodné veličiny,
jsou
nezávislé náhodné veličiny, 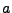 je skalár):
1. součet nezávislých náhodných veličin,
2. skalární násobek
je skalár):
1. součet nezávislých náhodných veličin,
2. skalární násobek
| 1. |
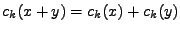 |
| 2. |
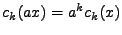 |
|
Jak je to se skalárním násobkem? Mějme náhodnou veličinu 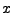 . Označme
. Označme
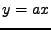 |
(11.14) |
náhodnou veličinu, která se od 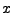 liší skalárním násobkem.
Objemové elementy se z (11.14) transformují
liší skalárním násobkem.
Objemové elementy se z (11.14) transformují
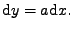 |
(11.15) |
Pravděpodobnost, že 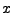 je v objemovém elementu
je v objemovém elementu
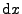 můžeme vyjádřit
můžeme vyjádřit
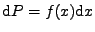 .
Pravděpodobnost, že
.
Pravděpodobnost, že 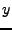 je v objemovém elementu
je v objemovém elementu
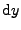 musí být totožná
musí být totožná
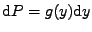 , neboť bijektivní zobrazení
(11.14) zobrazuje objemový element
, neboť bijektivní zobrazení
(11.14) zobrazuje objemový element
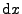 na objemový element
na objemový element
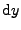 (tedy
(tedy 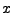 je v
je v
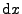 právě tehdy, když
právě tehdy, když
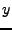 je v
je v
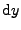 ). Z rovnosti
). Z rovnosti
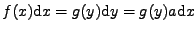 dostáváme pro hustoty
dostáváme pro hustoty
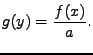 |
(11.16) |
Nyní určíme vztah mezi charakteristickými funkcemi
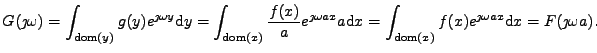 |
(11.17) |
Rovnají se tedy i logaritmy
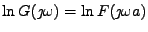 .
Obě strany nahradíme Taylorovým rozvojem
.
Obě strany nahradíme Taylorovým rozvojem
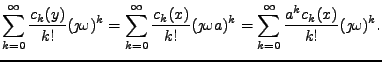 |
(11.18) |
Z rovnosti obou polynomů plyne
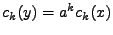 , viz. též druhá
vlastnost v tabulce 11.2.
, viz. též druhá
vlastnost v tabulce 11.2.
Momenty umíme odhadovat jednoduše jako výběrové průměry.
Jak ale odhadneme kumulanty? Rozepíšeme (11.11) pomocí vztahu
pro derivaci složené funkce. Tím se zbavíme logaritmu a zbydou
pouze derivace charakteristické funkce v nule, které se podle
(11.10) dají zapsat jako momenty.
Nejprve si ale vyčíslíme poěkud neobvyklý moment 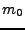 (budeme ho rovněž pro vyjádření kumulantů potřebovat)
(budeme ho rovněž pro vyjádření kumulantů potřebovat)
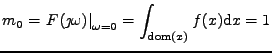 |
(11.19) |
Nyní již uvedu vyjádření několika prvních kumulantů pomocí momentů
U prvních třech případů jsem uvedl i jak dopadne derivace před
dosazením nuly za 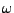 , pak je uveden výsledek po dosazení
(tedy vyjádření pomocí momentů) a nakonec je uvedeno zjednodušení
pro nulovou střední hodnotu
, pak je uveden výsledek po dosazení
(tedy vyjádření pomocí momentů) a nakonec je uvedeno zjednodušení
pro nulovou střední hodnotu 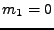 .
.
Kumulanty lichých řádů nebývají příliš výrazné
(téměř neviditelné modré průběhy na Obr. 10.3
znázorňují průběh 3. kumulantu na směru), proto je k separaci nepoužijeme.
První kumulant, který přichází v úvahu je kumulant 4. řádu (špičatost).
Na obrázcích Obr. 10.3, Obr. 10.6
je průběh tohoto kumulantu znázorněn fialovou barvou.
Vidíme, že jeho průběh nabývá v nezávislých směrech maxima
(kromě složek s normálním rozdělením Obr. 10.5,
kde jsou všechny kumulanty
vyšších řádů nulové).
Nezávislé směry (
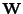 ) budeme tedy hledat jako směry maximalizující
4. kumulant.
) budeme tedy hledat jako směry maximalizující
4. kumulant.
Nejprve ale uvedu vysvětlení (trochu přesnější než odkaz na pár obrázků)
proč je 4. kumulant v nezávislých směrech maximální. Omezím se však pouze
na případ směsi dvou nezávislých procesů (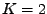 ).
).
Jelikož
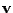 se od vektoru
se od vektoru
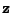 (případně
(případně
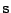 )
s nezávislými směry liší pouze ortogonální transformací (v dvourozměrném
případě otočením), musí být již ve
)
s nezávislými směry liší pouze ortogonální transformací (v dvourozměrném
případě otočením), musí být již ve
 nezávislé směry
na sebe kolmé11.3.
Jak je naznačeno na obrázku Obr. 11.1.
nezávislé směry
na sebe kolmé11.3.
Jak je naznačeno na obrázku Obr. 11.1.
Figure 11.1:
K výpočtu kumulantu na směru
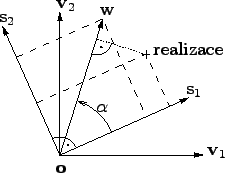 |
Jsou zde jednak vidět bázové vektory
 ,
,
 prostoru realizací náhodného vektoru
prostoru realizací náhodného vektoru
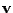 jejichž směry jsem
zvolil shodně se standardní bází a dále bázové vektory
jejichž směry jsem
zvolil shodně se standardní bází a dále bázové vektory
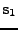 ,
,
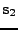 prostoru realizací náhodného vektoru
prostoru realizací náhodného vektoru
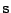 jež
jsou oproti
jež
jsou oproti
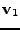 ,
,
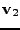 pouze otočené.
Zavedu směrový vektor
pouze otočené.
Zavedu směrový vektor
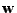 ,
,
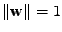 . V dourozměrném
případě je dán jediným parametrem - úhlem
. V dourozměrném
případě je dán jediným parametrem - úhlem
![$ \mathbf{w}^T =
[\cos \alpha, \sin \alpha]$](img812.png) .
Vše budu vyjadřovat vzhledem k bázi
.
Vše budu vyjadřovat vzhledem k bázi
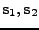 , jak
je naznačeno na obrázku (
, jak
je naznačeno na obrázku (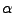 budu měřit od
budu měřit od
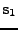 ),
neb je to přehlednější (nezávislé směry pak vychází v úhlech
0,
),
neb je to přehlednější (nezávislé směry pak vychází v úhlech
0, 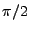 ). Nyní spočtu kolmý průmět
). Nyní spočtu kolmý průmět
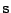 do
do
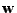 ,
a určím jeho
,
a určím jeho 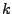 -tý kumulant (použiji přitom vlastnosti z tabulky
11.2)
-tý kumulant (použiji přitom vlastnosti z tabulky
11.2)
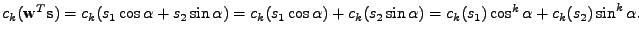 |
(11.21) |
Průběh funkcí
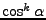 ,
,
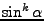 na
na 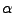 pro sudé
pro sudé
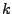 je znázorněn na Obr. 11.2.
je znázorněn na Obr. 11.2.
Figure 11.2:
Pro 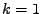 (žlutá),
(žlutá), 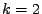 (červená),
(červená), 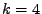 (modrá),
(modrá), 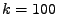 (zelená) (zleva doprava): průběh funkcí
(zelená) (zleva doprava): průběh funkcí
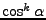 ,
,
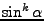 na
na 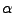 ,
průběh součtu
,
průběh součtu
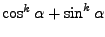 na
na 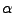 (pro
(pro
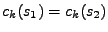 průběh
průběh 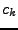 na
na 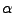 , až na měřítko),
průběh součtu
, až na měřítko),
průběh součtu
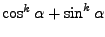 na
na 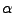 v polárních souřadnicích,
průběh mocniny
v polárních souřadnicích,
průběh mocniny 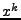 na
na
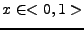
|
|
Vidíte, že s rostoucí mocninou jsou maxima průběhů stále výraznější.
Je to dáno průběhem mocniny na intervalu 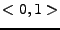 . Graf mocniny vždy
prochází body
. Graf mocniny vždy
prochází body ![$ [0,0]$](img820.png) a
a ![$ [1,1]$](img821.png) a s rostoucím
a s rostoucím 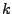 se stále více na intervalu
se stále více na intervalu
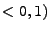 přimyká k 0. Polohy maxim jsou shodné s nezávislými
směry
přimyká k 0. Polohy maxim jsou shodné s nezávislými
směry 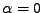 ,
,
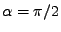 , atd..
Pro případ
, atd..
Pro případ 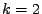 můžeme ještě obdržet konstantní průběh kumulantu na směru
můžeme ještě obdržet konstantní průběh kumulantu na směru
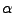 (kružnici v polárních souřadnicích), jsou-li kumulanty
(kružnici v polárních souřadnicích), jsou-li kumulanty
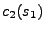 a
a
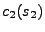 shodné (
shodné (
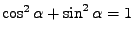 ),
ale pro vyšší
),
ale pro vyšší 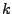 jsou již extrémy v nezávislých směrech jasně patrné
viz. Obr. 11.2
průběh součtu (
jsou již extrémy v nezávislých směrech jasně patrné
viz. Obr. 11.2
průběh součtu (
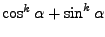 - až na měřítko průběh
pro shodné kumulanty) na
- až na měřítko průběh
pro shodné kumulanty) na 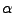 .
.
11.1.1 Fast ICA
Úkolem této části je uvedení jednoho algoritmu, který dokáže
nalézt směr maximalizující 4. kumulant (špičatost).
Nechť 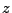 je náhodná proměná s nulovou střední hodnotou
je náhodná proměná s nulovou střední hodnotou
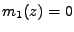 (vždy můžeme dosáhnout centrováním)
její špičatost můžeme vyjádříme z (11.20) pomocí momentů
(vždy můžeme dosáhnout centrováním)
její špičatost můžeme vyjádříme z (11.20) pomocí momentů
![$\displaystyle c_4(z) = m_4(z) - 3 m_2^2(z) = \mathrm{E}[z^4] - 3 \mathrm{E}^2[z^2] .$](img830.png) |
(11.22) |
Naším úkolem je najít směr
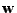 ,
,
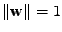 ,
pro který je
,
pro který je
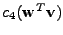 (špičatost kolmého průmětu
(špičatost kolmého průmětu
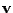 do onoho směru) extremální.
Vidíme, že možná řešení
do onoho směru) extremální.
Vidíme, že možná řešení
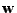 jsou omezeny podmínkou
jsou omezeny podmínkou
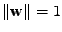 . Jedná se tedy o hledání vázaného extrému.
Pro řešení úlohy použijeme metodu Lagrangeových multiplikátorů.
K účelové funkci tedy přidáme násobek vazební podmínky v
implicitním tvaru
. Jedná se tedy o hledání vázaného extrému.
Pro řešení úlohy použijeme metodu Lagrangeových multiplikátorů.
K účelové funkci tedy přidáme násobek vazební podmínky v
implicitním tvaru
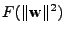 (
(
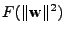 může být
například
může být
například
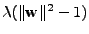 ,
, 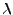 se nazývá Lagrangeův
součinitel)
se nazývá Lagrangeův
součinitel)
![$\displaystyle J = c_4(\mathbf{w}^T \mathbf{v}) + F(\Vert\mathbf{w}\Vert^2) = \m...
...})^4] - 3 \mathrm{E}^2[(\mathbf{w}^T \mathbf{v})^2] + F(\Vert\mathbf{w}\Vert^2)$](img834.png) |
(11.23) |
Nyní vypočteme gradient
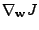 . Výpočet provedu pro jednotlivé
výrazy v (11.23) zvlášť, bude to přehlednější
. Výpočet provedu pro jednotlivé
výrazy v (11.23) zvlášť, bude to přehlednější
![$\displaystyle \frac{\partial \mathrm{E}[(\mathbf{w}^T \mathbf{v})^4]}{\partial ...
... \partial \mathbf{w}}] = 4 \mathrm{E}[(\mathbf{w}^T \mathbf{v})^3 \mathbf{v} ],$](img836.png) |
(11.24) |
Před výpočtem gradientu druhého výrazu ho nejprve trochu zjednodušímme
použitím (11.4)
![$\displaystyle \mathrm{E}[(\mathbf{w}^T \mathbf{v})^2] = \mathrm{E}[(\mathbf{w}^...
...^T \mathbf{R}_{vv} \mathbf{w} = \mathbf{w}^T\mathbf{w} = \Vert\mathbf{w}\Vert^2$](img837.png) |
(11.25) |
a spočteme gradient z
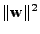
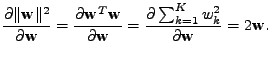 |
(11.26) |
Teď již uvedu gradient 2. výrazu (násobení 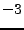 přidám nakonec)
přidám nakonec)
![$\displaystyle \frac{\partial \mathrm{E}^2[(\mathbf{w}^T \mathbf{v})^2]}{\partia...
...} = 2 \Vert\mathbf{w}\Vert^2 2 \mathbf{w} = 4 \Vert\mathbf{w}\Vert^2 \mathbf{w}$](img841.png) |
(11.27) |
Nakonec poslední 3. výraz
 |
(11.28) |
kde jsem označil
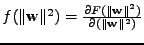 .
Sečtením všech tří výrazů (11.24), (11.27)
a (11.28) obdržíme gradient
.
Sečtením všech tří výrazů (11.24), (11.27)
a (11.28) obdržíme gradient
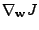 . Položíme ho rovný
. Položíme ho rovný
 (hledáme extém)
(hledáme extém)
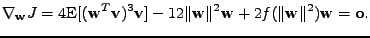 |
(11.29) |
Z tého rovnice asi
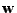 jednoduše nevyjádříme.
Vyjádříme tedy alespoň člen
jednoduše nevyjádříme.
Vyjádříme tedy alespoň člen
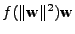 a postavíme rekurzi
pro
a postavíme rekurzi
pro
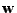
![$\displaystyle \mathbf{w}[k+1] = - \frac{2}{f(\Vert\mathbf{w}[k]\Vert^2)} \times...
...k]^T\mathbf{v})^3\mathbf{v}] - 3 \Vert\mathbf{w}[k]\Vert^2 \mathbf{w} \right) .$](img846.png) |
(11.30) |
V uvedené rekurzi zatím neumíme vyjádřit pouze skalár před 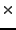 .
Jelikož ale hledáme řešení pouze s velikostí 1, není ho potřeba vyjadřovat,
budeme prostě normovat v každém kroku.
Je zřejmé (z toho jak jsme rekurzi postavili), že hledaná řešení
jsou pevnými body rekurze (je-li
.
Jelikož ale hledáme řešení pouze s velikostí 1, není ho potřeba vyjadřovat,
budeme prostě normovat v každém kroku.
Je zřejmé (z toho jak jsme rekurzi postavili), že hledaná řešení
jsou pevnými body rekurze (je-li
![$ \mathbf{w}[k]$](img848.png) řešení vyjde
řešení vyjde
![$ \mathbf{w}[k+1]$](img849.png) shodné - po normování na velikost 1).
Dá se dokázat že zvolíme-li libovolné
shodné - po normování na velikost 1).
Dá se dokázat že zvolíme-li libovolné
![$ \mathbf{w}[0]$](img850.png) , posloupnost
, posloupnost
![$ \{\mathbf{w}[k]\}_{k=0}^{\infty}$](img851.png) konverguje k těmto pevným bodům,
tedy k hledaným řešením. Uvedená rekurze konverguje velice rychle
obvykle stačí 10 iterací.
konverguje k těmto pevným bodům,
tedy k hledaným řešením. Uvedená rekurze konverguje velice rychle
obvykle stačí 10 iterací.
Nyní celý postup shrnu
Table 11.3:
Fast ICA algoritmus
![\begin{table}\begin{tabbing}
1. \= Zvolíme libovolný $\mathbf{w}[0]$, $\Vert\m...
...
skonči, jinak zvyš $k$\ o 1 a opakuj od bodu 2. \\
\end{tabbing}
\end{table}](img852.png) |
Podmínka v kroku 4. se dá přeložit takto: liší-li se
![$ \mathbf{w}^T[k+1]$](img853.png) od
od
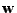 již velmi málo ukonči rekurzi.
Skalární součin v podmínce má (vzhledem normování obou vektorů)
význam kosinu úhlu mezi vektory. Jsou-li oba směry shodné vychází úhel
0 a absolutní hodnota je tedy 0.
již velmi málo ukonči rekurzi.
Skalární součin v podmínce má (vzhledem normování obou vektorů)
význam kosinu úhlu mezi vektory. Jsou-li oba směry shodné vychází úhel
0 a absolutní hodnota je tedy 0.
Cvičení 11.0: Cílem bude dokončit separaci pro úlohy A2,C2
s neortogonální regulární mixážní maticí z minulého cvičení 10.0.1.
Impementujte Fast ICA algoritmus viz. tabulka 11.3
k nalezení jednoho z nezávislých směrů
![$ \mathbf{w}^T =[ w_1, w_2 ]$](img854.png) . Protože víte, že nezávislé směry
jsou na sebe kolmé jednoduše určíte zbývající nezávislý směr
(prohodíte složky a u jedné obrátíte znaménko).
Sestavíte z nich hledanou matici
. Protože víte, že nezávislé směry
jsou na sebe kolmé jednoduše určíte zbývající nezávislý směr
(prohodíte složky a u jedné obrátíte znaménko).
Sestavíte z nich hledanou matici
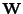
![$\displaystyle \mathbf{W}^T = \left[ \begin{array}{cc} w_1 & -w_2 \\ w_2 & w_1 \\ \end{array} \right] .$](img855.png) |
(11.31) |
Určete realizace náhodného vektoru
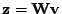 . Mělo by dojít k obnovení
původních nezávislých složek vektoru
. Mělo by dojít k obnovení
původních nezávislých složek vektoru
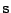 .
.
Vypište (vyneste) si hledaný směr na iteraci a chybu na iteraci.
Vyneste si graf realizací náhodného vektoru
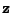 i s
transformovanou bazí (puvodní standardní baze
i s
transformovanou bazí (puvodní standardní baze
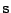 ) by se měla
transformovat opět na standardní bázi
) by se měla
transformovat opět na standardní bázi
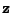 .
Vyneste si průbeh separovaných složek na realizaci (vzorku).
V případě řečových signálů si poslechněte výsledek.
.
Vyneste si průbeh separovaných složek na realizaci (vzorku).
V případě řečových signálů si poslechněte výsledek.
Uvádím zde implementaci rekurze v Matlabu (vstupem je vybělené
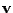 ,
, 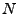 značí počet vzorků původních nahodných procesů, nebo
počet realizací náhodných vektorů po zjednodušení):
značí počet vzorků původních nahodných procesů, nebo
počet realizací náhodných vektorů po zjednodušení):
ITER = 10; % pocitam pevny pocet iteraci (bez podminky)
w = zeros(2,ITER); % smer na iteraci
e = zeros(1,ITER); % chyba na iteraci
w(:,1) = [1;0]; % pocatecni podminka
for n = 2:ITER
w(:,n) = -(sum(v.*(ones(2,1)*(w(:,n-1)'*v).^3 ),2)/N - 3*w(:,n-1));
w(:,n) = w(:,n)/sqrt(w(:,n)'*w(:,n)); % normovani
e(n) = w(:,n)'*w(:,n-1) - 1; % chyba
end;
w % vypis smeru
e % vypis chyby (mela by jit k 0)
Výsledky pro A2:
Figure:
Úloha A2 harmonický signál a realizace bílého stacionárního procesu s
rovnoměrně rozloženými vzorky, regulární-neortogonální mixážní matice:
(zleva doprava)
graf realizací náhodného vektoru
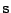 (zelene) a nezávislé směry
(standardní báze - modře),
graf realizací náhodného vektoru
(zelene) a nezávislé směry
(standardní báze - modře),
graf realizací náhodného vektoru
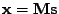 a nezávislé směry (modře) a
variance na směru s vlastními směry (červeně),
graf realizací náhodného vektoru
a nezávislé směry (modře) a
variance na směru s vlastními směry (červeně),
graf realizací náhodného vektoru
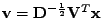 a nezávislé směry (modře) dale variance (červeně) a špičatost (fialová)
na směru,
graf realizací náhodného vektoru
a nezávislé směry (modře) dale variance (červeně) a špičatost (fialová)
na směru,
graf realizací náhodného vektoru
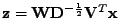 a nezávislé směry (modře) dále variance (červeně) a špičatost (fialová)
na směru
a nezávislé směry (modře) dále variance (červeně) a špičatost (fialová)
na směru
|
|
Figure:
Úloha A2 harmonický signál a realizace bílého stacionárního procesu s
rovnoměrně rozloženými vzorky, regulární-neortogonální mixážní matice:
časové průběhy po aplikaci
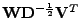 (
(
![$ \mathbf{z}[n]$](img861.png) )
)
|
|
Výsledky pro C2:
Figure:
Úloha C2 řečové signály, regulární-neortogonální mixážní matice:
(zleva doprava)
graf realizací náhodného vektoru
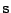 (zelene) a nezávislé směry
(standardní báze - modře),
graf realizací náhodného vektoru
(zelene) a nezávislé směry
(standardní báze - modře),
graf realizací náhodného vektoru
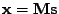 a nezávislé směry (modře) a
variance na směru s vlastními směry (červeně),
graf realizací náhodného vektoru
a nezávislé směry (modře) a
variance na směru s vlastními směry (červeně),
graf realizací náhodného vektoru
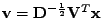 a nezávislé směry (modře) dale variance (červeně) a špičatost (fialová)
na směru,
graf realizací náhodného vektoru
a nezávislé směry (modře) dale variance (červeně) a špičatost (fialová)
na směru,
graf realizací náhodného vektoru
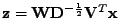 a nezávislé směry (modře) dále variance (červeně) a špičatost (fialová)
na směru
a nezávislé směry (modře) dále variance (červeně) a špičatost (fialová)
na směru
|
|
Figure:
Úloha C2 řečové signály,
regulární-neortogonální mixážní matice:
časové průběhy po aplikaci
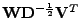 (
(
![$ \mathbf{z}[n]$](img861.png) )
)
|
|


Next: 12. Cvičení 12: Směrový
Up: 11. Cvičení 11: Dokončení
Previous: 11. Cvičení 11: Dokončení
Mirek
2006-12-12
![]() nenajdeme
(pro jakékoli ortogonální
nenajdeme
(pro jakékoli ortogonální
![]() jsou složky
jsou složky
![]() dekorelované).
Musíme tedy sáhnout po statistikách vyšších řádů.
dekorelované).
Musíme tedy sáhnout po statistikách vyšších řádů.
![]() ).
Mějme náhodnou veličinu
).
Mějme náhodnou veličinu ![]() její hustotu
pravděpodobnosti označíme
její hustotu
pravděpodobnosti označíme ![]() a charakteristickou funkci
a charakteristickou funkci
![]() (Fourierovu transformaci
(Fourierovu transformaci ![]() )
)
![]() lze z (11.1)
lze rozepsat jako lineární kombinace
nezávislých náhodných veličin. Hledání
lze z (11.1)
lze rozepsat jako lineární kombinace
nezávislých náhodných veličin. Hledání
![]() znamená vlastně nalézt
koeficienty lineárních kombinací. Proto nás zajímá, zda se tyto operace
dají pomocí momentů jednoduše vyjádřit.
Lineární kombinaci
nezávislých náhodných veličin mohu vždy rozepsat pomocí součtu nezávislých
náhodných veličin a skalárního násobku.
Co se při těchto operacích děje s momenty?
Jelikož známe vztah charakteristické funkce a momentů je odpověď
jednoduchá.
znamená vlastně nalézt
koeficienty lineárních kombinací. Proto nás zajímá, zda se tyto operace
dají pomocí momentů jednoduše vyjádřit.
Lineární kombinaci
nezávislých náhodných veličin mohu vždy rozepsat pomocí součtu nezávislých
náhodných veličin a skalárního násobku.
Co se při těchto operacích děje s momenty?
Jelikož známe vztah charakteristické funkce a momentů je odpověď
jednoduchá.
![]() a
a ![]() , jejich součet označíme
, jejich součet označíme
![]() . Hustoty pravděpodobnosti označím
. Hustoty pravděpodobnosti označím
![]() ,
, ![]() a
a ![]() . Charakteristické funkce označím velkými písmeny
jak jsme zvyklí u obrazů Fourierovy transformace
. Charakteristické funkce označím velkými písmeny
jak jsme zvyklí u obrazů Fourierovy transformace
![]() ,
,
![]() ,
,
![]() . Tabulka 11.1 uvádí
co se děje s hustotami, charakteristickými funkcemi, atd. při
součtu nezávislých náhodných veličin.
. Tabulka 11.1 uvádí
co se děje s hustotami, charakteristickými funkcemi, atd. při
součtu nezávislých náhodných veličin.
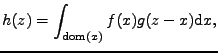
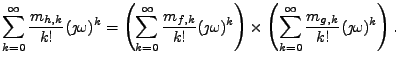
![]() (budeme ho rovněž pro vyjádření kumulantů potřebovat)
(budeme ho rovněž pro vyjádření kumulantů potřebovat)
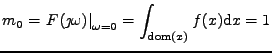
![]() ) budeme tedy hledat jako směry maximalizující
4. kumulant.
) budeme tedy hledat jako směry maximalizující
4. kumulant.
![]() ).
).
![]() se od vektoru
se od vektoru
![]() (případně
(případně
![]() )
s nezávislými směry liší pouze ortogonální transformací (v dvourozměrném
případě otočením), musí být již ve
)
s nezávislými směry liší pouze ortogonální transformací (v dvourozměrném
případě otočením), musí být již ve
![]() nezávislé směry
na sebe kolmé11.3.
Jak je naznačeno na obrázku Obr. 11.1.
nezávislé směry
na sebe kolmé11.3.
Jak je naznačeno na obrázku Obr. 11.1.
![\includegraphics[width=10cm]{ada11/obrmat/fig10.ps}](img818.png)
![]() je náhodná proměná s nulovou střední hodnotou
je náhodná proměná s nulovou střední hodnotou
![]() (vždy můžeme dosáhnout centrováním)
její špičatost můžeme vyjádříme z (11.20) pomocí momentů
(vždy můžeme dosáhnout centrováním)
její špičatost můžeme vyjádříme z (11.20) pomocí momentů
![]() . Protože víte, že nezávislé směry
jsou na sebe kolmé jednoduše určíte zbývající nezávislý směr
(prohodíte složky a u jedné obrátíte znaménko).
Sestavíte z nich hledanou matici
. Protože víte, že nezávislé směry
jsou na sebe kolmé jednoduše určíte zbývající nezávislý směr
(prohodíte složky a u jedné obrátíte znaménko).
Sestavíte z nich hledanou matici
![]()
![]() i s
transformovanou bazí (puvodní standardní baze
i s
transformovanou bazí (puvodní standardní baze
![]() ) by se měla
transformovat opět na standardní bázi
) by se měla
transformovat opět na standardní bázi
![]() .
Vyneste si průbeh separovaných složek na realizaci (vzorku).
V případě řečových signálů si poslechněte výsledek.
.
Vyneste si průbeh separovaných složek na realizaci (vzorku).
V případě řečových signálů si poslechněte výsledek.
![]() ,
, ![]() značí počet vzorků původních nahodných procesů, nebo
počet realizací náhodných vektorů po zjednodušení):
značí počet vzorků původních nahodných procesů, nebo
počet realizací náhodných vektorů po zjednodušení):
![\includegraphics[width=10cm]{ada11/obrmat/fig1.ps}](img857.png)
![\includegraphics[width=10cm]{ada11/obrmat/fig2.ps}](img859.png)
![\includegraphics[width=10cm]{ada11/obrmat/fig3.ps}](img862.png)
![\includegraphics[width=10cm]{ada11/obrmat/fig4.ps}](img863.png)