1.2 Odhady momentů - vlastní náplň cvičení

Než budeme cokoliv odhadovat musíme si nejprve vygenerovat nějaký zajímavý signál, na kterém naše odhady budeme zkoušet. Náš signál definujeme jako signál $x[n]$ na výstupu filtru uvedeného na Obr. 1.1 při buzení (signál $v[n]$) bílým stacionární gusovským procesem s nulovou střední hodnotou a rozptylem jedna.

Figure 1.1: Modelování signálu $x[n]$, pro $n<1000$ platí $k_1=0.9$,$k_2=0.5$, pro $n \ge 1000$ platí $k_1=0.0$,$k_2=1.0$

Jelikož umíme pracovat pouze s posloupnostmi konečné délky omezíme se na náhodný vektor délky $N = 2000$ (s identicky normálně rozloženými složkami, kde normální rozdělení má nulovou střední hodnotu a rozptyl jedna). Takový jednoduše získáme použitím randn(N,1).

Cvičení 1.0: Vaším úkolem je vygenerovat $x[n]$, $n = 1\ldots N$, za předpokladu že $x[0] = 0$ (počáteční podmínky).

Zkuste si napsat skript pro generování signálu $x$ sami. Až když budete mít potíže, prohlédněte si následující skript.

% genx.m
N = 2000;
L = 1000;
v = randn(N,1);
x = zeros(N,1);

k1 = 0.9;
k2 = 0.5;
x(1) = v(1)*k2; % index -1 by vyvolal chybu, musime resit zvlast
for n = 2:N
  if n == L+1
    k1 = 0.0;
    k2 = 1.0;
  end
  x(n) = k1*x(n-1) + k2*v(n);
end

Takto by to asi napsal čtenář předchozího úvodu. Lze to zapsat take jednodušeji použitím funkce filter(B,A,u). Vstupní parametry B, resp. A mají význam koeficientů polynomů čitatele resp. jmenovatele přenosové funkce, viz. help filter. Nejdříve tedy musíme zjistit jaký vztah májí koeficienty 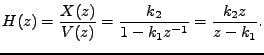$k_1$ a $k_2$ k těmto polynomům. Napíšeme rovnici filtru v časové oblasti

$$x[n] = k_1 x[n-1] + k_2 v[n].$$

Nyní použijeme Z-transformaci^1.1

$$X(z) = k_1 X(z) z^{-1} + k_2 V(z).$$

Dále vyjádříme přenosovou funkci filtru (poměr obrazů výstupu a vstupu filtru)

$$H(z) = \frac{X(z)}{V(z)} = \frac{k_2}{1 - k_1 z^{-1}} = \frac{k_2 z}{z - k_1}.$$

S použitím funkce filter bychom $x[n]$ vygenerovali asi takto:

s = [ filter([0.5, 0],[1,-0.9],v(1:L)); filter([1, 0],[1, 0],v(L+1:N)) ];

Cvičení 1.1: Nyní si průběhy $x[n]$ a $v[n]$ vyneste.

To můžeme udělat např. přidámím těchto řádků k genx.m:

figure(1)        % budeme kreslit do obrazku 1
plot(1:N,v,'b'); % horizontalni souradnice vynasenych bodu,
                 % vertikalni souradnice vynasenych bodu, barva
hold on % prubehy budou kresleny "pres sebe"
plot(1:N,x,'r');
hold off         % vypnuti kresleni "pres sebe"
xlabel('n');     % popisy os
ylabel('x[n],v[n]');
title('namodelovany signal x[n] (cervene)');

Figure 1.2: Namodelovaný signál

1.2.1 Některé důležité momenty

Momenty definujeme pomocí operátoru střední hodnoty $\mathrm{E}[.]$ ^1.2.

Střední hodnotu náhodného procesu $x[n]$ n čase $n$ značíme $E[x[n]]$. Pro stacionární proces se momenty s časem nemění a platí tedy $\mathrm{E}[x[n]] = \mathrm{E}[x[n-1]]$, značení se pak většinou zjednodušuje na $\mathrm{E}[x]$.

1.2.1.1 Momenty druhého řádu

Dále budeme předpokládat nulové střední hodnoty náhodných procesů $x[n]$, $y[n]$, případně náhodných veličin $x$ a $y$. Vzájemná korelace n. v. $x$ a $y$ definujeme jako $\mathrm{E}[xy]$. Matici vzájemných korelací náhodných procesů $x[n]$ a $y[n]$ definujeme (zde uvádím pouze rozmě r $2\times2$)

$$\mathbf{R}_{xy}[n] = \left[ \begin{array}{cc} \mathrm{E}[x[n... ...{E}[x[n-1]y[n]] & \mathrm{E}[x[n-1]y[n-1]] \end{array}\right].$$

Autokorelační matici náhodného procesu $x[n]$definujeme (zde uvádím pouze rozměr $2\times2$)

$$\mathbf{R}_{xx}[n] = \left[ \begin{array}{cc} \mathrm{E}[x[n... ...E}[x[n-1]x[n]] & \mathrm{E}[x[n-1]x[n-1]] \end{array}\right].$$

Na diagonále nalezneme rozpltyly. Všiměte si, že matice je symetrická. Jestliže je proces $x[n]$ stacionární je navíc ekvidiagonální:

$$\mathbf{R}_{xx} = \left[ \begin{array}{cc} r_{xx,0} & r_{xx,1} \\ r_{xx,1} & r_{xx,0} \end{array}\right]$$

Kde $r_{xx,k} = \mathrm{E}[x[n]x[n-k]]$.

1.2.1.2 Momenty vyšších řádů - předpokládáme nulové střední hodnoty

Momenty 3. a 4. řádu ( $\mathrm{E}[x^3]$, $\mathrm{E}[x^4]$) budeme používat k výpočtu kumulantů šikmosti a špičatosti při slepé separaci signálů pomocí ICA (Independent Component Analysis).

1.2.2 Odhady pomocí výběrových průměrů

Jestliže je proces stacionární a ergodický lze jeho momenty odhadovat průměrováním v čase. Velkou výhodou je, že si pak vystačíme pouze s jedinou realizací. Odhad daného momentu obdržíme tak, že operátor střední hodnoty jednoduše nahradíme půměrem v čase. Například střední hodnotu $\mathrm{E}[x[n]]$ odhadneme jako $\hat{\mu} = \frac{1}{N} \sum_{n=1}^{N} x[n]$, korelaci $\mathrm{E}[x[n]x[n-1]]$ odhadneme jako $\hat{r}_{xx,1} = \frac{1}{N} \sum_{n=1}^{N} x[n] x[n-1]$ nebo moment vyššího řádu $\mathrm{E}[(x[n])^3 x[n-2]]$ odhadneme jako $\frac{1}{N} \sum_{n=1}^{N} (x[n])^3 x[n-2]$.

1.2.2.1 Blokový odhad

Při blokovém odhadu předpokládáme stacionaritu v rámci bloků typicky fixní délky. V rámci každého bloku odhadneme momenty průměrováním.

Cvičení 1.2: Odhadněte autokorelační matici $x[n]$ blokovým odhadem. Použijte bloky délky $500$.

Řešení s for-cyklem:

M = 500;        % délka bloku
B = floor(N/M); % počet bloků

rxx0 = zeros(B,1); % inicializace koeficientů Rxx
rxx1 = zeros(B,1);

for b = 1:B
  for n= ((b-1)*M+2):M*b
    rxx0(b) = rxx0(b) + x(n)^2/(M-1);
    rxx1(b) = rxx1(b) + x(n)*x(n-1)/(M-1);
  end
end

Řešení bez for-cyklu (pouze náhrada za vnitřní smyčku):

  range = ((b-1)*M+2):M*b;
  X = [ x(range) , x(range-1) ];
  Rxx = X'*X/(M-1);
  rxx0(b) = Rxx(1,1);
  rxx1(b) = Rxx(1,2);

Vynesení obrázků:

figure(2)
subplot(2,1,1) % subplot umoznuje dát více grafů do
               % jednoho obrazku, 1. podgraf
plot(1:N,x,'b');
subplot(2,1,2) % 2. podgraf
plot(1,0,'b'); % jenom kvuli pouziti hold on
hold on
for b = 1:B
nz = (b-1)*M+1 ;
nk = M*b ;
plot([nz,nk],[rxx0(b),rxx0(b)],'b');
plot([nz,nk],[rxx1(b),rxx1(b)],'r');
end
hold off

Figure: Blokový odhad $\mathbf{R}_{xx}$

1.2.2.2 Průběžný odhad

K odhadu střední hodnoty lze využít strukturu integrátoru na Obr. 1.4.

Figure 1.4: Realizace operátoru střední hodnoty pomocí integrátoru

Otázka je jaká volba $k_1$,$k_2$ poskytne dobrý odhad střední hodnoty. Shrneme nejprve požadavky na frekvenční charakteristiku: Frekvenční charakteristika by měla mít maximum na nulové frekvenci, ostatní frekvence by měly být pokud možno potlačeny. Hodnota frekvenční charakteristiky v tomto maximu by měla být jedna (chceme střední hodnotu a ne nějaký násobek). Systém by měl být stabilní.

Řešením této úlohy dojdeme k tomu, že možné hodnoty konstant $k_1$,$k_2$ musí být reálné a dále musí splňovat podmínky $k_1 \in (0,1)$, a $k_2 = 1 - k_1$. Takovýto integrátor se nazývá normalizovaný. Obvykle se jeho koeficienty značí $\lambda$ místo $k_1$, a $1 - \lambda$ místo $k_2$. Odhad, který je jako zde aktualizován s každým novým vzorkem budeme nazývat průběžný.

Cvičení 1.3: Zkuste najít správné řešení sami.

Cvičení 1.4: Vyneste si frekvenční charakteristiku, impulsovou odezvu a póly a nuly v z-rovině pro různé hodnoty pro různé hodnoty $k_1$,$k_2$.

Implulsovou odezvu vypočtete jednoduše pomocí funkce filter ^1.3 nebo impz. Dále můžete použít následující funkce Matlabu.

H = freqz(B,A,W)

vypočte vektor hodnot frekvenční charakteristky na frekvencích daných vektorem W (radiány). B a A jsou opět hodnoty koeficientů polynomů čitatele a jmenovatele přenosové funkce jako u funkce filter.

Poznámka: Takovouto funkci si jednoduše můžete vytvořit sami. Stačí když si vzpomenete, že frekvenční charakteristika (systému diskrétního v čase) je vlastně přenosová funkce vyčíslená na jednotkové kružnici. pro integrátor by to dopadlo takto:

H = zeros(length(W),1); % length vraci velikost vektoru
for k = 1:length(W)
  z = exp(j*W(k));
  H(k) = k2*z/(z-k1);
end

Nebo trochu zhuštěně:

z = exp(j*W);
H = k2*z ./ (z-k1); % vyznam operatoru "./",".*",".^" je, ze operace
                    % se provadi prvek po prvku, operandy pak musi
                    % byt matice stejneho rozmeru, vyzkousekjte si

zplane(B,A)

vynese póly a nuly přenosové funkce do z-roviny. B a A mají opět stejný význam jako u funkce filter.

Figure 1.5: Frekvenční charakteristika, impulsová odezva, přenosová funkce pro normalizovaný integrátor ( $\lambda = 0.8$)

Cvičení 1.5: Odhadněte autokorelační matici $x[n]$ průběžným odhadem pomocí normalizovaného integrátoru. Vyzkoušejte vliv $\lambda$ na odhad (volte např. $\lambda = 0.5, 0.95, 0.995$ ).

Řešení:

lambda = 0.995; % koeficienty normalizovaneho integratoru
k1 = lambda;
k2 = 1-lambda;

rxx0 = zeros(N,1);
rxx1 = zeros(N,1);

rxx0(1) = k2*x(n)^2;
rxx1(1) = k2*x(n)*x(n-1);

for n= 2:N
  rxx0(n) = k1*rxx0(n-1) + k2*x(n)^2;
  rxx1(n) = k1*rxx1(n-1) + k2*x(n)*x(n-1);
end

Figure: Průběžný odhad $\mathbf{R}_{xx}$, byl použit normalizovaný integrátor s $\lambda = 0.995$