- ... Sovka1
-
Tyto stránky částečně čerpají ze
starší verze stránek
pro cvičení od Romana Čmejly a Pavla Sovky.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Z-transformaci1.1
- Zde jen krátce uvedu, že
Z-transformace definovaná
![$ X(z) = \sum_{n=0}^{\infty} x[n] z^n$](img103.png) , je
lineární, dále zpoždění předmětu (
, je
lineární, dále zpoždění předmětu (![$ x[n]$](img1.png) ) o
) o 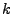 vzorků se v obraze
projeví násobením obrazu nezpožděného předmětu (
vzorků se v obraze
projeví násobením obrazu nezpožděného předmětu (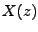 ) faktorem
) faktorem 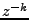 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
1.2
- Pro spojitě rozloženou n. v.
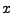 s hustotou pravděpodobnosti
s hustotou pravděpodobnosti
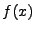 střední hodnotu definujeme
střední hodnotu definujeme
![$ \mathrm{E}[x] = \intop_{-\infty}^{\infty}x f(x) \mathrm{d}x$](img112.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...filter
1.3
-
Nápověda: Uvědomte si, že impulsová odezva je výstup systému
pri buzení jednotkovým impulsem při nulových počátečních podmínkách.
Chceme-li prvních 100 vzorků impulsové odezvy stačí zavolat
filter(B,A,[1; zeros(99,1)]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... přesnosti?2.1
-
Ktomu abyste zjistili, který z odhadů je více lokální si
uvědomte, které vzorky pro dané
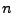 k odhadu nejvíce přispívají.
U průběžného odhadu se jedná o LTI systém a tedy hodnoty odhadu
pro různá
k odhadu nejvíce přispívají.
U průběžného odhadu se jedná o LTI systém a tedy hodnoty odhadu
pro různá 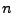 obdržíme konvolucí s impulsovou odezvou, vzpomeňte
si jak vypadala, viz. 1. cvičení.
U rekurentního odhadu si pořádně prohlédněte rekurzi a zjistíte,
že hodnota odhadu pro dané
obdržíme konvolucí s impulsovou odezvou, vzpomeňte
si jak vypadala, viz. 1. cvičení.
U rekurentního odhadu si pořádně prohlédněte rekurzi a zjistíte,
že hodnota odhadu pro dané 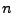 je střední hodnota vzorků
je střední hodnota vzorků
![$ x[1],\ldots,x[n]$](img148.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... přednášce2.2
-
Z (2.1),(2.2) lze jednoduše sestavit věrohodnost
pro parametry
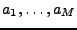 a
a 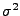 , a určit ML odhad
AR koeficientů, když tak učiníte zjistíte, že tento odhad je shodný
se zde uvedeným (nejmenší čtverce).
, a určit ML odhad
AR koeficientů, když tak učiníte zjistíte, že tento odhad je shodný
se zde uvedeným (nejmenší čtverce).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
2.3
-
Zde lze již název predikce signálu
![$ x_p[n]$](img11.png) lépe zdůvodnit.
Minimalizací disperze
lépe zdůvodnit.
Minimalizací disperze ![$ e[n]$](img13.png) se vlastně snažíme, aby
se vlastně snažíme, aby
![$ x_p[n]$](img11.png) byla
byla ![$ x[n]$](img1.png) co nejblíž. Z (2.5) je vidět, že
co nejblíž. Z (2.5) je vidět, že ![$ x_p[n]$](img11.png) je konstruována pouze s použitím minulých vzorků
je konstruována pouze s použitím minulých vzorků ![$ x[n]$](img1.png) (
(![$ x[n-1]$](img164.png) ,
, ![$ x[n-2]$](img165.png) , ...) nikoli
, ...) nikoli ![$ x[n]$](img1.png) samotného
(lze tedy vyčíslit již v čase
samotného
(lze tedy vyčíslit již v čase 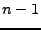 ), odtud název predikce
), odtud název predikce ![$ x[n]$](img1.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (gradient)2.4
-
Když Vám nebude jasné, jak se dospělo k derivaci výrazu
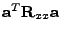 , uvědomte si předně,
že
, uvědomte si předně,
že
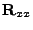 jako autokorelační matice musí být symetrická
(
jako autokorelační matice musí být symetrická
(
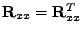 ).
Dále si
rozepište součin
).
Dále si
rozepište součin
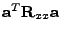 pro rozměr matice
pro rozměr matice 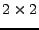 pomocí prvků
pomocí prvků
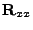 (ze symetrie
vystačíte pouze se třemi symboly) a složek
(ze symetrie
vystačíte pouze se třemi symboly) a složek
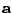 .
Roznásobte a jednoduše zderivujte podle první
složky vektoru
.
Roznásobte a jednoduše zderivujte podle první
složky vektoru
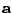 a pak podle druhé. Uspořádáte-li
výsledeky do sloupcového vektoru, vyjde Vám vektor
a pak podle druhé. Uspořádáte-li
výsledeky do sloupcového vektoru, vyjde Vám vektor
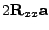 . Uvidíte, že výsledek
. Uvidíte, že výsledek
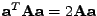 pro
pro
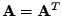 lze jednoduše zobecnit pro jakýkoli rozměr
lze jednoduše zobecnit pro jakýkoli rozměr
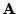 . Derivace výrazu
. Derivace výrazu
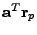 , je již
mnohem jednodušší úloha.
, je již
mnohem jednodušší úloha.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... blok2.5
- Vyberte si nějaký, kde je řečový signál výrazný.
Zkuste také volit znělý, neznělý blok.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...specgram(y)2.6
- Funkce specgram bohužel vytváří trochu
špatně časovou osu (podívejte se na obrázek).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
3.1
-
Inverze vztahu dopadne přesně takto
ale protože nám příliš nepůjde o počáteční fázi, omezím se zde na
použití neurčitého integrálu.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gradientu3.2
- Gradient udává směr
(zde v prostoru vah)
ve kterém funkce (zde
![$ e^2[n]$](img169.png) ) roste nejrychleji.
) roste nejrychleji.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... popisováno3.3
- Jestli někomu chybí 2 z gradientu lze zahrnout do
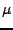 (konstantu
(konstantu 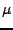 jsem kvůli tomu nepřeznačoval)
jsem kvůli tomu nepřeznačoval)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
3.4
-
Přesně filtr s proměnnými vahami nemusí mít nuly, není totiž LTI a nemusí
mít vůbec přenosovou funkci (ale najdou se výjimky).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...plant_A
4.1
- neznámý systém se obvykle označuje jako plant (kytička).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... povrch4.2
-
Všimněte si, že váhy nemají již index
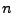 , označením
, označením
![$ \mathrm{E}[e^2[n]](\mathbf{w})$](img286.png) míníme MSE pro fixní váhy filtru
(v ustáleném stavu)
míníme MSE pro fixní váhy filtru
(v ustáleném stavu)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... predikovat5.1
-
Adaptivní filtr v Obr. 5.1
vytváří lineární kombinaci minulých vzorků vstupu
![$ x[n]$](img1.png) tedy predikci
tedy predikci ![$ x_p[n]$](img11.png) . Chyba
. Chyba
![$ e[n]$](img13.png) vzniká tak, že se od vstupu
vzniká tak, že se od vstupu ![$ x[n]$](img1.png) odčítá jeho predikce
odčítá jeho predikce ![$ x_p[n]$](img11.png) ,
proto zde má predikovatelnost velký význam pro minimalizaci
,
proto zde má predikovatelnost velký význam pro minimalizaci
![$ \mathrm{E}[e^2[n]]$](img221.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
jednoznačná7.1
-
Sloupcové vektory
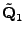 tvoří ortonormální bázi
doplňku
tvoří ortonormální bázi
doplňku
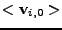 k
k
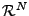 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... determinantu7.2
-
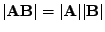
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... typu7.3
-
Rozklad se nazývá vlastním rozkladem matice
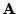 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
7.4
-
Existenci
![$ \mathbf{P}^{\frac{1}{2}}[n-1]$](img576.png) dokážeme následovně.
Jelikož
dokážeme následovně.
Jelikož
![$ \mathbf{P}[n-1]$](img575.png) symetrická, existuje její vlastní rozklad, viz.
lemma 7.5
symetrická, existuje její vlastní rozklad, viz.
lemma 7.5
![$ \mathbf{P}[n-1] = \mathbf{V} \mathbf{D} \mathbf{V}^T$](img578.png) ,
kde
,
kde
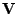 je ortogonální (
je ortogonální (
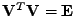 ) a
) a
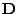 je diagonální. Definuji matici
je diagonální. Definuji matici
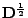 jako diagonální matici jež má na diagonále odmocněné diagonální prvky
jako diagonální matici jež má na diagonále odmocněné diagonální prvky
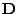 (povšiměte si, že
(povšiměte si, že
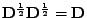 ).
Matici
).
Matici
![$ \mathbf{P}^{\frac{1}{2}}[n-1]$](img576.png) požadovaných vlastností pak sestrojím
takto
požadovaných vlastností pak sestrojím
takto
![$ \mathbf{P}^{\frac{1}{2}}[n-1]
= \mathbf{V} \mathbf{D}^{\frac{1}{2}} \mathbf{V}^T$](img581.png) . Uvedená matice je
jistě symetrická (
. Uvedená matice je
jistě symetrická (
![$ (\mathbf{P}^{\frac{1}{2}}[n-1])^T
= \mathbf{P}^{\frac{1}{2}}[n-1]$](img582.png) ) a z ortogonality
) a z ortogonality
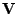 platí
platí
![$ (\mathbf{P}^{\frac{1}{2}}[n-1])\mathbf{P}^{\frac{1}{2}}[n-1]
=
\mathbf{V} \mat...
...rac{1}{2}} \mathbf{V}^T
=
\mathbf{V} \mathbf{D} \mathbf{V}^T
=
\mathbf{P}[n-1]
$](img583.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... závorky7.5
-
Platí
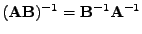 (utvořte součin levé a pravé strany rovnosti).
(utvořte součin levé a pravé strany rovnosti).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... přiblížení8.1
-
Pro pomalu měnící se váhy (dostatečně malé
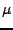 ) mohu systém považovat
přibližně za LTI s váhami
) mohu systém považovat
přibližně za LTI s váhami
![$ c_1[n],c_2[n]$](img611.png) pro nějaké malé okolí
času
pro nějaké malé okolí
času 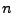 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kaskády8.2
-
Impulsová odezva celé kaskády je dána jako konvoluce
impulsových odezev obou prediktorů a konvoluce je komutativní
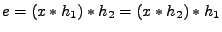 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variancí10.1
-
Předpoklady nulových středních hodnot nenulových variancí jsou zde
kvůli zpřehlednění výkladu (při výpočtu rozptylů nemusíme odečítat střední
hodnoty, pro nenulové rozptyly vychází jednodušší struktura vlastního rozkladu
korelačních matic). Jejich vynecháním lze obdržet obecněji
aplikovatelné výsledky.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inverze10.2
-
Všiměte si, že jsouli náhodné veličiny
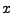 ,
,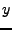 nezávislé,
pak jsou nezávislé i
nezávislé,
pak jsou nezávislé i 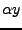 ,
,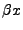 (
(
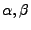 jsou nějaké
reálné konstanty).
jsou nějaké
reálné konstanty).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... prvek10.3
-
Při násobení jednotkovou maticí
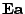 se zachovává všechno
(měřítka i pořadí složek
se zachovává všechno
(měřítka i pořadí složek
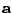 ).
Proházení (permutaci) složek výsledku dosáhneme také proházením řádků
).
Proházení (permutaci) složek výsledku dosáhneme také proházením řádků
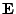 . Všiměte si, že vzniklou matici pak můžete charakterizovat tak,
že má v každém řádku a sloupci právě jednu jedničku.
Taková matice se nazývá permutační (provádí permutaci složek
. Všiměte si, že vzniklou matici pak můžete charakterizovat tak,
že má v každém řádku a sloupci právě jednu jedničku.
Taková matice se nazývá permutační (provádí permutaci složek
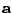 ).
Připustíme-li navíc změnu měřítka, máme naši definici separační matice.
).
Připustíme-li navíc změnu měřítka, máme naši definici separační matice.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\space 10.4
- To poznáme
tak, že neumíme sestrojit významě odlišnou matici
(která se neliší pouze permutacemi a měřítky)
pro kterou jsou separované složky rovněž nezávislé.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... složek11.1
-
Nelze nalézt
jinou významě odlišnou transformaci (lišící se i jinak než permutací
a měřítky složek) uvedených vlastností (poskytne vektor s nezávislými
složkami).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ukázat11.2
-
Záměna derivace a integrálu není samozřejmá (záměna dvou limit),
ale zde je možná.
Vysvětlení neuvádím.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kolmé11.3
-
Všiměte si, že jakákoli ortogonální transformace
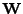 zachvává
skalární součin
zachvává
skalární součin
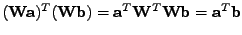 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
12.1
-
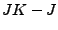 je dimenze
je dimenze
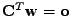 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.