

Next: 7.6 Konvergence střední hodnoty
Up: 7. Cvičení 7: Konvergenční
Previous: 7.4 NLMS
Subsections
7.5 Úvod do vlastního rozkladu symetrických matic
Než začneme, definujeme některé pojmy, které se budou později hodit.
Hermitovskou traspozici značím 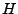 v horním indexu nad
symbolem matice, má význam transpozice matice a nahrazení prvků
matice jejich komplexně sdruženými verzemi
v horním indexu nad
symbolem matice, má význam transpozice matice a nahrazení prvků
matice jejich komplexně sdruženými verzemi
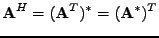 |
(7.15) |
Jak vidíte pro reálnou matici (vektor) se hermitovská transpozice od
obyčejné transpozice neliší. Vektory chápu jako matice se speciálním
rozměrem (jeden řádek, nebo jeden sloupec). Vztahem (7.15)
je tedy hermitovská
transpozice zavedena i pro vektory.
Frobeniovu normu matice
 značím
značím
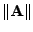 a
definuji ji následujícím způsobem
a
definuji ji následujícím způsobem
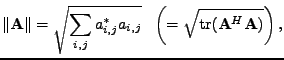 |
(7.16) |
kde součet jde přes všechny prvky 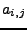 matice
matice
 .
Tím je Frobeniova norma definována rověž pro vektory. Je-li
.
Tím je Frobeniova norma definována rověž pro vektory. Je-li
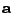 sloupcový, lze (7.16)
zjednodušit (odmocnica ze skalárního součinu)
sloupcový, lze (7.16)
zjednodušit (odmocnica ze skalárního součinu)
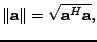 |
(7.17) |
je-li navíc reálný
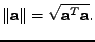 |
(7.18) |
Mějme vektor
![$ \mathbf{h}^T = [h_1,\ldots, h_N] \in \mathcal{R}^N$](img422.png) a reálnou matici
a reálnou matici
 o rozměru
o rozměru 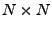 .
Funkce typu
.
Funkce typu
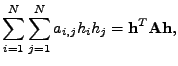 |
(7.19) |
kde 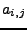 značím prvky
značím prvky
 se nazývá kvadratickou formou
v
se nazývá kvadratickou formou
v
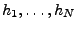 . Všiměte si, že je-li
. Všiměte si, že je-li
 nesymetrická
mohu ji nahradit symetrickou
nesymetrická
mohu ji nahradit symetrickou
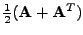 aniž by se funkce (7.19) (kvadratická forma) změnila.
Při studiu kvadratických forem v reálných proměnných (
aniž by se funkce (7.19) (kvadratická forma) změnila.
Při studiu kvadratických forem v reálných proměnných (
 )
tedy stačí omezíme-li se na reálné symetrické matice
)
tedy stačí omezíme-li se na reálné symetrické matice
 .
.
Chybový povrch
![$ \mathrm{E}[e^2[n]](\mathbf{w})$](img286.png) se dá zapsat jako kvadratická forma (povšiměte si výrazu
se dá zapsat jako kvadratická forma (povšiměte si výrazu
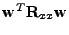 v (4.4)).
Studovat chybový povrch znamená tedy studovat kvadratickou formu,
případně reálné symetrické matice (autokorelační matice
v (4.4)).
Studovat chybový povrch znamená tedy studovat kvadratickou formu,
případně reálné symetrické matice (autokorelační matice
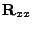 je reálná symetrická).
V dalším textu se tedy zaměřím a omezím na studium
reálných symetrických matic.
Připomínám, že matice je symetrická právě tehdy, když
je reálná symetrická).
V dalším textu se tedy zaměřím a omezím na studium
reálných symetrických matic.
Připomínám, že matice je symetrická právě tehdy, když
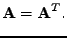 |
(7.20) |
(prvky symetricky umístěné vzhledem k diagonále jsou shodné
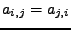 ).
).
Uvedu zde jeden výsledek, který se nám bude později hodit.
Mějme komplexní vektor
![$ \mathbf{h}^T = [h_1,\ldots, h_N] \in \mathcal{C}^N$](img430.png) a reálnou symetrickou matici
a reálnou symetrickou matici
 (
(
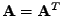 ) o rozměru
) o rozměru 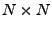 .
Pak platí
.
Pak platí
Reálná čtvercová matice
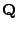 se nazývá ortogonální
právě tehdy, když
se nazývá ortogonální
právě tehdy, když
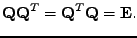 |
(7.22) |
Ekvivalentně se dá říci, že sloupcové vektory tvoří ortonormální bázi
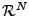 , kde
, kde 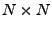 je rozměr
je rozměr
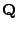 (rozepište si
maticový součin pomocí skalárních součinů sloupců
(rozepište si
maticový součin pomocí skalárních součinů sloupců
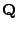 ).
Zavedeme-li označení
).
Zavedeme-li označení
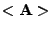 pro lineární obal sloupců matice
pro lineární obal sloupců matice
 , lze uvedené tvrzení zapsat jednodušeji takto
, lze uvedené tvrzení zapsat jednodušeji takto
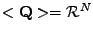 .
Povšiměte si, že z (7.22) a jednoznačnosti inverze rovněž plyne
.
Povšiměte si, že z (7.22) a jednoznačnosti inverze rovněž plyne
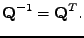 |
(7.23) |
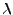 nazveme vlastním číslem matice
nazveme vlastním číslem matice
 právě tehdy, když existuje vektor
právě tehdy, když existuje vektor
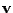 tak,
že platí
tak,
že platí
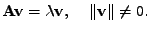 |
(7.24) |
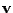 pak nazýváme vlastním vektorem matice
pak nazýváme vlastním vektorem matice
 příslušným
vlastnímu číslu
příslušným
vlastnímu číslu 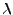 .
.
Odečtením pravé strany můžeme (7.24) přepsat
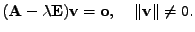 |
(7.25) |
Vlastní vektory příslušné vlastímu číslu 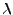 tedy
tvoří lineární prostor (až na vyjmuté triviální řešení
tedy
tvoří lineární prostor (až na vyjmuté triviální řešení
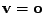 ) dimenze větší nebo rovné 1 (alespoň jedno
netriviální řešení musí existovat, abychom
) dimenze větší nebo rovné 1 (alespoň jedno
netriviální řešení musí existovat, abychom  prohlásili za
vlastní číslo). Proto se při hledání vlastních vektorů stačí omezit
na hledání ortonormálních bází, tohoto lineárního prostoru.
Označením vlastní vektor budu tedy mínit i to, že daný vektor má
normu 1.
prohlásili za
vlastní číslo). Proto se při hledání vlastních vektorů stačí omezit
na hledání ortonormálních bází, tohoto lineárního prostoru.
Označením vlastní vektor budu tedy mínit i to, že daný vektor má
normu 1.
Pokusme se nyní nalézt vlastní čísla matice
 o
rozměru
o
rozměru 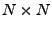 .
Aby rovnice (7.25) poskytla nějaká netriviální řešení
.
Aby rovnice (7.25) poskytla nějaká netriviální řešení
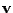 (podmínka pro vlastní číslo), musí mít matice
(podmínka pro vlastní číslo), musí mít matice
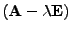 lineárně závislé
sloupce (složky
lineárně závislé
sloupce (složky
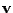 můžeme chápat jako koeficienty
v lineární kombinaci sloupcových vektorů matice), tedy
matice
můžeme chápat jako koeficienty
v lineární kombinaci sloupcových vektorů matice), tedy
matice
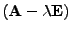 musí být nutně singulární.
Tuto podmínku lze jednoduše zapsat pomocí jejího determinantu
musí být nutně singulární.
Tuto podmínku lze jednoduše zapsat pomocí jejího determinantu
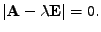 |
(7.26) |
Polynom v 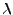 na levé straně se nazývá charakteristický polynom
matice
na levé straně se nazývá charakteristický polynom
matice
 . Snadno nahlédnete, že má stupeň
. Snadno nahlédnete, že má stupeň 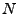 (
(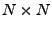 je rozměr
je rozměr
 ) z definice determinantu. Platí tedy následující
lemma.
) z definice determinantu. Platí tedy následující
lemma.
Lemma 7.1
Vlastních čísel matice
 o rozměru
o rozměru 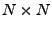 je
je 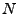 (včetně násobnosti).
Vlastní čísla reálné symetrické matice jsou reálná nebo komplexně
sdružená.
(včetně násobnosti).
Vlastní čísla reálné symetrické matice jsou reálná nebo komplexně
sdružená.
Proof.
[ ]
Důkaz:Plyne jednoduše z toho, že vlastní čísla matice

jsou kořeny jejího charakteristického polynomu.

Lemma 7.2
Vlastní čísla reálné symetrické matice
 jsou reálná, a vlastní vektory
příslušné vlastním číslům
jsou reálná, a vlastní vektory
příslušné vlastním číslům
 mají reálné složky.
mají reálné složky.
Proof.
[ ]
Důkaz:Z předchozího lemmatu
7.1 víme, že vlastní čísla

mohou být komplexní. Vezměme libovolné vlastní číslo

(z
7.1 víme, že existuje)
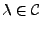
.
A jeden k
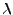
příslušný vlastní vektor
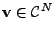
(opět víme, že
existuje, jinak by
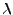
nebylo vlastní číslo

), kde
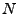
je
rozměr

.
Z (
7.25) musíme uvažovat komplexní vektor,
neboť máme komplexní
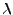
.
Utvořme součin
Vyjádříme
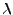
Reálnost čitatele jsme ověřili v (
7.21) jmenovatel je dokonce
reálný kladný. Tedy
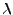
je reálné a z (
7.25) jsou reálné
i k němu příslušné vlastní vektory.

Lemma 7.3
Vlastní vektory příslušné různým vlastním číslům reálné symetrické
matice
 jsou navzájem ortogonální.
jsou navzájem ortogonální.
Proof.
[ ]
Důkaz:Nechť
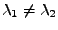
jsou vlastní čísla

.
Existují tedy vektory
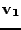
,
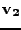
(k nim příslušné vlasní vektory) tak , že
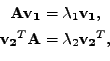 |
(7.27) |
(druhou rovnost jsem pouze transponoval a použil symetrii

).
Součin
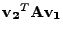
pak můžeme zjednodušit
různými způsoby, podle toho, kterou z rovností (
7.27)
použijeme
tedy
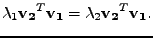 |
(7.29) |
Je-li skalární součin
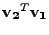
různý od 0,
můžeme jím vydělit a dostáváme ihned spor
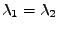
.
Proto musí být skalární součin
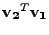
nutně nulový
a oba vektory jsou tedy navzájem ortogonální.

Lemma 7.4
Nechť 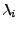 je vlastní číslo násobnosti
je vlastní číslo násobnosti 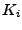 reálné symetrické matice
reálné symetrické matice
 o rozměru
o rozměru 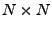 , pak dimenze prostoru řešení (7.25)
je rovna
, pak dimenze prostoru řešení (7.25)
je rovna 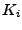 .
.
Závěr věty lze formulovat ekvivaleně takto:
Maximální počet lineárně nezávislých vlastních vektorů příslušných
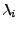 je roven
je roven 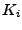 . Nebo,
hodnost
. Nebo,
hodnost
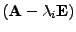 je
je 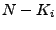 .
.
Proof.
[ ]
Důkaz:Nechť platí předpoklad tvrzení. Dokážu, že ke každému
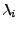
lze nalézt
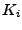
lineárně nezávislých vektorů. Z lematu
7.3
pak plyne, že tento
počet nemůže být vyšší (jinak by prostory řešení (
7.25)
pro různá vlastní čísla nebyly navzájem ortogonálními
podprostory
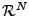
).
Označme
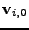 vlastní vektor příslušný k
vlastní vektor příslušný k 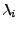 (z (7.24) víme, že jeden určitě existuje).
(z (7.24) víme, že jeden určitě existuje).
Utvořme ortogonální matici
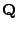
![\begin{displaymath}\begin{gathered}\mathbf{Q}_1 = [ \mathbf{v}_{i,0} \vert \tild...
...1 ],\\ \mathbf{Q}_1^T \mathbf{Q}_1 = \mathbf{E}. \end{gathered}\end{displaymath}](img463.png) |
(7.30) |
Povšiměte si, že volba
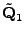
není nijak
jednoznačná
7.1.
Utvořme součin
![$\displaystyle \mathbf{Q}_1^T \mathbf{A} \mathbf{Q}_1 = \left[ \begin{array}{c} ...
...t c} \lambda_i & \mathbf{o}^T \\ \mathbf{o} & \mathbf{A}_1 \end{array}\right] .$](img466.png) |
(7.31) |
V posledním kroku jsem označil
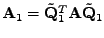
.
Použitím (
7.30) a vlastností determinantu
7.2.
dostaneme
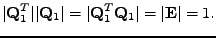 |
(7.32) |
S použitím (
7.32), (
7.31)
(a stejné vlastnosti determinantu)
nyní můžeme zapsat charakteristický polynom

pomocí
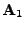
Z (
7.33)
plyne, že násobnost
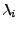
pro
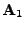
se oproti

snížila o 1 tedy na
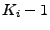
(jestliže
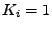
tak
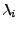
vůbec není vlastním číslem
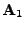
)
jinak mají
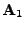
a

všechna ostatní vlastní čísla
totožná včetně násobností.
V případě, že 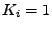 jsme již
jsme již 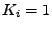 vlastních lineárně nezávislých
vlastních vektorů našli a jsme hotovi.
V opačném případě postupujeme následovně.
Jelikož
vlastních lineárně nezávislých
vlastních vektorů našli a jsme hotovi.
V opačném případě postupujeme následovně.
Jelikož
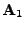 má vlastní číslo
má vlastní číslo 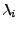 , existuje
k němu příslušný vlastní vektor. Označme ho
, existuje
k němu příslušný vlastní vektor. Označme ho
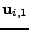 .
Tvrdím, že vektor
.
Tvrdím, že vektor
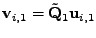 je vlastním vektorem
je vlastním vektorem

ortogonálním k
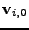
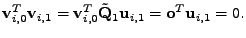 |
(7.35) |
Nyní můžeme postup opakovat, s tím, že v
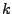
-tém kroku volíme
ortogonální matici
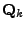
způsobem
![$ \mathbf{Q}_k =
[ \mathbf{\mathbf{v}_{i,0}},\ldots,\mathbf{\mathbf{v}_{i,k-1}}
\vert\tilde{\mathbf{Q}}_k ]$](img479.png)
dokud
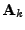
má vlastní číslo
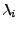
.
Uvedený způsobem získáme právě
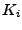
navzájem ortonormálních
vektorů příslušných
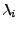
.

Proof.
[ ]
Důkaz:I.
Nechť

má
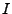
různých vlastních čísel

.
Z lemmatu
7.4 víme, že pro dané vlastní číslo
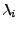
tvoří vlastní vektory

lineární prostor s dimenzí rovnou
násobnosti tohoto vlastního čísla
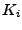
.
Můžeme tedy vybrat
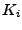
vlastních vektorů tvořících ortonormální bázi tohoto prostoru.
Označme je
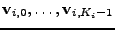
.
Učiňme tak pro všechna vlastní čísla. Celkem jsme tedy vybrali
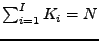
vlastních vektorů. Tyto vektory jsou navzájem ortonormální.
Ortonormalitu v rámci
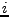
-té skupiny
(vlastních vektorů příslušných
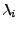
) jsme zajistili vhodnou volbu
a ornormalita pro různá
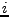
(pro různá vlastní čísla)
plyne z lemmatu
7.3.
Tvoří tedy bázi
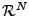
navíc ortonormální.
Mohu z nich tedy sestavit ortogonální matici
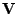
tak, že vybrané vlastní vektory tvoří sloupce
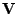
![$\displaystyle \mathbf{V} = [ \mathbf{v}_{1,0},\mathbf{v}_{1,1}\ldots,\mathbf{v}_{1,K_1-1},\ldots, \mathbf{v}_{I,K_I-1} ].$](img489.png) |
(7.37) |
Utvořme součin
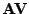
a použijme (
7.24)
![$\displaystyle \mathbf{A}\mathbf{V} = [ \lambda_1\mathbf{v}_{1,0},\lambda_1\math...
...,1}\ldots,\lambda_1\mathbf{v}_{1,K_1-1},\ldots, \lambda_I\mathbf{v}_{I,K_I-1} ]$](img491.png) |
(7.38) |
Jedná se vlastně o matici
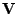
s přenásobenými sloupci,
to lze jednodušeji zapsat přenásobením diagonální maticí zprava
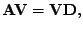 |
(7.39) |
kde
![$\displaystyle \mathbf{D} = \mathrm{diag}([ \lambda_1,\lambda_1,\ldots,\lambda_1\ldots,\lambda_I ]).$](img493.png) |
(7.40) |
Vynásobením (
7.38)
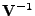
zprava (z (
7.23) lze zapsat i jako
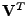
neboť
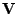
je ortogonální) dostáváme rozklad
(
7.36)
matice

požadovaných vlastností.
II.
Mějme libovolnou dvojcí matic
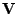 ,
,
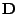 ,
kde
,
kde
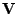 je ortogonální a
je ortogonální a
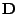 diagonální,
splnující (7.36).
Vynásobením (7.36)
diagonální,
splnující (7.36).
Vynásobením (7.36)
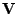 zprava získáme
zprava získáme
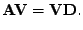 |
(7.41) |
Označme sloupce
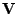
, a diagonální prvky
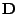
kde
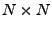
je rozměr obou matic.
Rozepišme rovnost (
7.41) pro jednotlivé sloupce
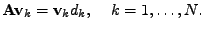 |
(7.42) |
Protože
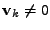
, neboť
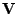
je ortogonální,
jsou podle (
7.24)
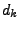
vlastními čísly matice

a
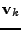
příslušnými vlastními vektory.
Nyní dokáži, že každé vlasní číslo
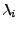
matice

je na diagonále
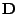
obsaženo nevýše tolikrát, kolik činí jeho násobnost
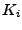
(to, že počet výskytů
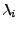
na diagonále
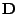
je právě
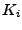
plyne pak jednonuše z toho, že diagonála
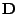
obsahuje pouze vlastní čísla
a počet prvků na diagonále je
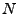
, což je počet všech vlastních čísel matice

včetně násobnosti).
Důkaz provedeme sporem.
Předpokládejme tedy, že počet výskytů
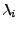
na diagonále
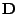
je
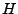
, kde
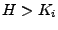
. Z (
7.42) tedy existuje
sloupců
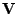
(označme je
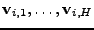
),
pro které platí
Z (
7.24) se jedná o vlastní vektory příslušné
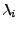
(
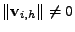
z ortogonality
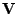
),
navíc jsou (z ortogonality
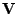
) tyto vektory lineárně nezávislé.
K
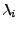
tedy přísluší více než
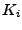
lineárně nezávislých vlastních
vektorů. To je ale spor s lemmatem
7.4.
Počet výskytů
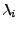
na
diagonále
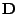
je tedy menší nebo roven
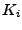
.

Lemma 7.6
Matice je regulární právě tehdy, když má pouze nenulová vlastní čísla.
Proof.
[ ]
Důkaz:Místo uvedeného tvrzení dokáži ekvivalentní:
Matice je singulární právě tehdy, když má nulové vlastní číslo.
Matice

má z definice (
7.24)
nulové vlasní číslo právě tehdy,
když existuje netriviální řešení
Tedy existuje netriviální lineární kombinace sloupců

jež
je rovna nulovému vektoru (sloupce

jsou lineárně závislé).
Tedy

je singulární.

Lemma 7.7
Matice
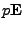 má jediné vlastní číslo
má jediné vlastní číslo 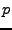 násobnosti
násobnosti 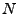 , kde
, kde
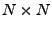 je rozměr matice.
je rozměr matice.
Proof.
[ ]
Důkaz:Jednoduše utvořím některý z vlastních rozkladů
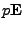
.
Například zvolím
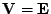
a
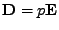
.
Snadno ověřím že se skutečně jedná o vlastní rozklad
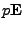
(
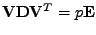
,
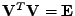
a
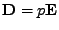
je diagonální).
Z lemmatu
7.5 musí být na diagonále
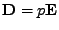
pouze
vlastní čísla
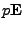
, kde počet výskytů daného vlastního čísla
je právě roven jeho násobnosti. Jelikož diagonála obsahuje pouze
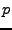
právě
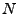
-krát, je
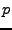
jediným vlastním číslem
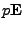
násobnosti
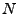

Lemma 7.8
Nechť
 je symetrická reálná matice rozměru
je symetrická reálná matice rozměru
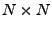 .
Kvadratická forma
.
Kvadratická forma
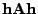 je nezáporná
(
je nezáporná
(
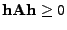 pro všechna
pro všechna
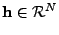 )
právě tehdy, když
)
právě tehdy, když
 má pouze nezáporná vlastní čísla.
má pouze nezáporná vlastní čísla.
Proof.
[ ]
Důkaz:Jelikož

je reálná symetrická, existuje z lematu
7.5
rozklad
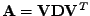
, kde
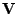
je ortogonální a
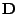
diagonální.
Navíc
![$ \mathbf{D} = \mathrm{diag}([\lambda_1,\ldots,\lambda_N])$](img517.png)
obsahuje na diagonále všechna vlastní čísla
matice

včetně násobností.
Součin
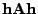
mohu nyní zapsat
kde jsem označil
![$ \mathbf{u} = [u_1, \ldots u_N]^T= \mathbf{V}^T\mathbf{h}$](img519.png)
.
Z (
7.43) plyne, že má-li

pouze nezáporná vlastní
čísla (
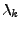
) nemůže být pravá strana záporná pro jakoukoliv volbu
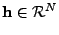
, tedy i levá strana musí být nezáporná.
Naopak, předpokládejme, že

má i záporná vlastní čísla,
nalezneme tedy
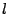
pro které je
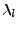
záporné. Sestrojíme takový
vektor
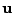
, který má
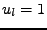
a ostatní složky nulové.
Jelikož je
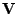
ortogonální (a tedy rovněž regulární),
jednoduše k
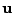
nalezneme vzor
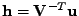
.
Tedy existuje
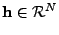
tak, že
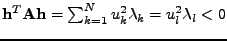
, což je spor.

Lemma 7.9
Nechť
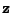 je reálný náhodný vektor.
Korelační matice
je reálný náhodný vektor.
Korelační matice
![$ \mathbf{R} = \mathrm{E}[\mathbf{x}\mathbf{x}^T]$](img528.png) ,
,
![$ \mathbf{x} = \mathbf{z} - \mathrm{E}[\mathbf{z}]$](img529.png) má pouze nezáporná vlastní čísla.
má pouze nezáporná vlastní čísla.
Proof.
[ ]
Důkaz:Předně
![$ \mathbf{R} = \mathrm{E}[\mathbf{x}\mathbf{x}^T]$](img528.png)
je zřejmě
reálná symetrická matice.
Zvolme libovolný
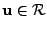
.
Pak, platí
kde jsem zavedl náhodnou proměnou
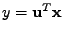
.
Kvadratická forma
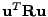
je tedy nezáporná,
takže
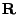
má podle lemmatu
7.8
pouze nezáporná vlastní čísla.

Nechť matice
 má rozměr
má rozměr 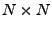 .
Stopu matice
.
Stopu matice
 značím
značím
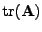 a
definuji jako součet
jejích diagonálních prvků
a
definuji jako součet
jejích diagonálních prvků
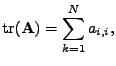 |
(7.44) |
kde 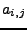 značím prvky
značím prvky
 .
.
Nechť
 má rozměr
má rozměr 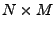 a
a
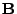 má rozměr
má rozměr 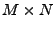 .
Označme
.
Označme
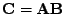 , pak platí
, pak platí
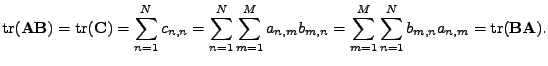 |
(7.45) |
Lemma 7.10
Nechť 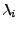 je vlastním číslem korelační matice
je vlastním číslem korelační matice
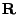 ,
pak
,
pak
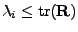
Proof.
[ ]
Důkaz:Jelikož korelační matice je reálná symetrická, existuje podle
lemmatu
7.5 rozklad
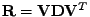
,
kde
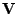
je ortogonální a
![$ \mathbf{D} = [\lambda_1,\ldots,\lambda_N]$](img544.png)
je diagonální
(diagonála matice
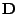
obsahuje pouze vlastní čísla
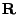
a to všechna
včetně násobnosti).
Dosaďme za
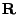
do
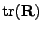
a použijme
(
7.45) a ortogonalitu
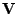
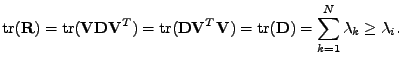 |
(7.46) |
V posledním kroku jsem použil lemma
7.9
(korelační matice má pouze nezáporná
vlastní čísla).

Shrnu nyní závěry o vlastních číslech korelačnich matic plynoucí
z lemmat 7.6 až 7.10.
Nechť
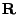 je libovolná korelační matice
je libovolná korelační matice
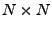 (autokorelační matice je speciální připad korelační matice) a
nechť
(autokorelační matice je speciální připad korelační matice) a
nechť
 jsou její různá vlastní čísla.
Uspořádejme je od nejmenšího k největšímu
jsou její různá vlastní čísla.
Uspořádejme je od nejmenšího k největšímu
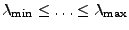 .
Z lemmatu 7.9 a lemmatu 7.10 plyne,
omezení na jejich hodnoty
.
Z lemmatu 7.9 a lemmatu 7.10 plyne,
omezení na jejich hodnoty
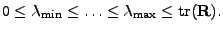 |
(7.47) |
Je-li navíc
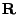 regulární lze dolní mez s použitím
lemmatu 7.6 trochu přiostřit
regulární lze dolní mez s použitím
lemmatu 7.6 trochu přiostřit
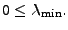 |
(7.48) |
Jedná-li se o autokorelační matici stacionárního náhodného
procesu ![$ x[n]$](img1.png) lze horní mez zapsat jako
lze horní mez zapsat jako 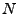 násobek jeho disperze
násobek jeho disperze
![$ r_{xx,0} = \mathrm{E}[(x[n] - \mathrm{E}(x[n]))^2]$](img550.png) (pro nulovou střední hodnotu a ergodický proces můžeme odhadovat jako
výkon)
(pro nulovou střední hodnotu a ergodický proces můžeme odhadovat jako
výkon)
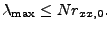 |
(7.49) |
Autokorelační matice bílých stacionárních procesů mají tvar
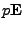 ,
a mají tedy z lemmatu 7.7
pouze jediné vlastní číslo násobnosti
,
a mají tedy z lemmatu 7.7
pouze jediné vlastní číslo násobnosti 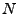 .
Naopak barevné procesy se vyznačují ruznými vlastními čísly.
Dokonce poměr
.
Naopak barevné procesy se vyznačují ruznými vlastními čísly.
Dokonce poměr
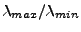 (eigenvalue spread)
lze brát jako jakousi míru barevnosti procesu.
(eigenvalue spread)
lze brát jako jakousi míru barevnosti procesu.


Next: 7.6 Konvergence střední hodnoty
Up: 7. Cvičení 7: Konvergenční
Previous: 7.4 NLMS
Mirek
2006-12-12
![]() se dá zapsat jako kvadratická forma (povšiměte si výrazu
se dá zapsat jako kvadratická forma (povšiměte si výrazu
![]() v (4.4)).
Studovat chybový povrch znamená tedy studovat kvadratickou formu,
případně reálné symetrické matice (autokorelační matice
v (4.4)).
Studovat chybový povrch znamená tedy studovat kvadratickou formu,
případně reálné symetrické matice (autokorelační matice
![]() je reálná symetrická).
V dalším textu se tedy zaměřím a omezím na studium
reálných symetrických matic.
Připomínám, že matice je symetrická právě tehdy, když
je reálná symetrická).
V dalším textu se tedy zaměřím a omezím na studium
reálných symetrických matic.
Připomínám, že matice je symetrická právě tehdy, když
![]() a reálnou symetrickou matici
a reálnou symetrickou matici
![]() (
(
![]() ) o rozměru
) o rozměru ![]() .
Pak platí
.
Pak platí
![]() nazveme vlastním číslem matice
nazveme vlastním číslem matice
![]() právě tehdy, když existuje vektor
právě tehdy, když existuje vektor
![]() tak,
že platí
tak,
že platí
![]() o
rozměru
o
rozměru ![]() .
Aby rovnice (7.25) poskytla nějaká netriviální řešení
.
Aby rovnice (7.25) poskytla nějaká netriviální řešení
![]() (podmínka pro vlastní číslo), musí mít matice
(podmínka pro vlastní číslo), musí mít matice
![]() lineárně závislé
sloupce (složky
lineárně závislé
sloupce (složky
![]() můžeme chápat jako koeficienty
v lineární kombinaci sloupcových vektorů matice), tedy
matice
můžeme chápat jako koeficienty
v lineární kombinaci sloupcových vektorů matice), tedy
matice
![]() musí být nutně singulární.
Tuto podmínku lze jednoduše zapsat pomocí jejího determinantu
musí být nutně singulární.
Tuto podmínku lze jednoduše zapsat pomocí jejího determinantu
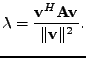
![]() je roven
je roven ![]() . Nebo,
hodnost
. Nebo,
hodnost
![]() je
je ![]() .
.
![]() vlastní vektor příslušný k
vlastní vektor příslušný k ![]() (z (7.24) víme, že jeden určitě existuje).
(z (7.24) víme, že jeden určitě existuje).
![]()
![]() jsme již
jsme již ![]() vlastních lineárně nezávislých
vlastních vektorů našli a jsme hotovi.
V opačném případě postupujeme následovně.
Jelikož
vlastních lineárně nezávislých
vlastních vektorů našli a jsme hotovi.
V opačném případě postupujeme následovně.
Jelikož
![]() má vlastní číslo
má vlastní číslo ![]() , existuje
k němu příslušný vlastní vektor. Označme ho
, existuje
k němu příslušný vlastní vektor. Označme ho
![]() .
Tvrdím, že vektor
.
Tvrdím, že vektor
![]() je vlastním vektorem
je vlastním vektorem
![]()
![]() typu (7.36)
výše uvedených vlastností, pak sloupcové vektory matice
typu (7.36)
výše uvedených vlastností, pak sloupcové vektory matice
![]() v rozkladu jsou
vlastními vektory
v rozkladu jsou
vlastními vektory
![]() a diagonální prvky matice
a diagonální prvky matice
![]() v rozkladu jsou vlastní čísla
v rozkladu jsou vlastní čísla
![]() (diagonála
(diagonála
![]() obsahuje
každé vlastní číslo
obsahuje
každé vlastní číslo
![]() právě tolikrát, kolik činí jeho násobnost).
Tím je
právě tolikrát, kolik činí jeho násobnost).
Tím je
![]() pro danou matici
pro danou matici
![]() určena jednoznačně,
až na permutaci diagonálních prvků.
určena jednoznačně,
až na permutaci diagonálních prvků.![]() ,
,
![]() ,
kde
,
kde
![]() je ortogonální a
je ortogonální a
![]() diagonální,
splnující (7.36).
Vynásobením (7.36)
diagonální,
splnující (7.36).
Vynásobením (7.36)
![]() zprava získáme
zprava získáme
![]() má rozměr
má rozměr ![]() .
Stopu matice
.
Stopu matice
![]() značím
značím
![]() a
definuji jako součet
jejích diagonálních prvků
a
definuji jako součet
jejích diagonálních prvků
![]() má rozměr
má rozměr ![]() a
a
![]() má rozměr
má rozměr ![]() .
Označme
.
Označme
![]() , pak platí
, pak platí
![]() je libovolná korelační matice
je libovolná korelační matice
![]() (autokorelační matice je speciální připad korelační matice) a
nechť
(autokorelační matice je speciální připad korelační matice) a
nechť
![]() jsou její různá vlastní čísla.
Uspořádejme je od nejmenšího k největšímu
jsou její různá vlastní čísla.
Uspořádejme je od nejmenšího k největšímu
![]() .
Z lemmatu 7.9 a lemmatu 7.10 plyne,
omezení na jejich hodnoty
.
Z lemmatu 7.9 a lemmatu 7.10 plyne,
omezení na jejich hodnoty